näillä sivuilla me tarkastelemme joitakin mielenkiintoisia käsitteitä, tarkastelemme kaareva tilaa: mitä kaareva avaruus tarkoittaa, miten voimme kertoa, jos tilaa on kaareva sen sisällä tai sen ulkopuolella.
katsomme, miten voimme upottaa tyypin tilaa toisen sisällä ja nähdä, että voimme kartoittaa eri välilyöntejä eri tavoin.
– Me myös tarkastelemme compacification ja miten voimme edustaa äärettömän suuri ja äärettömän pieni vektorit meidän tiloihin tavalla, joka ei johda erikoisen ja muita ongelmia.,
nämä käsitteet osoittautuvat hyödyllisiksi, vaikka työskentelemme litteän tilan kanssa, löydämme tapoja edustaa vektoreita ja lentokoneita, jotka eivät käy läpi alkuperää. Tämä antaa meille tapoja edustaa rotaatioita ja käännöksiä yhtenä operaationa.
toinen sovellus on relativistinen avaruusaika.
Rienmannilainen geometria
Rienmannilaisessa geometriassa avaruus voi käyristyä eri paikoissa (KS.manifoldit) tässä tarkastellaan geometrioita, joissa avaruuden käyrä on vakio.,
Eulidean Geometria
taulu tilaa
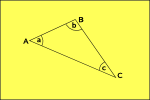
Hyperbolinen Geometria
tilaa käyrät ulospäin,
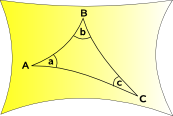
Pallomainen Geometria ja Elliptinen Geometria
tilaa käyrät sisäänpäin
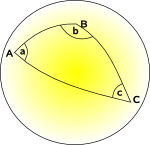
kaareva (epäeuklidinen) geometria emme voi löytää koordinaatit, jotka ovat toisiaan vastaan kohtisuorassa, missä koordinoida linjat ovat rinnakkain toisiaan ja jossa jokainen ruudukon neliö on samalla alueella., Voimme ehkä löytää koordinaattijärjestelmän, jossa voimme tehdä joitakin näistä, mutta emme kaikkia.
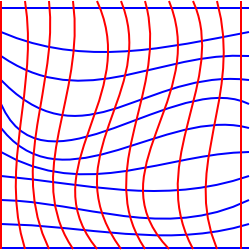
Tämä kaavio pyrkii havainnollistamaan tätä tilannetta 2 mitat, vaikka sen hieman harhaanjohtava, koska olemme tehneet sen koneeseen niin meillä voisi olla piirretty suorakaiteen koordinaatit.
yrittää havainnollistaa tilannetta, jossa tämä on mahdotonta, voimme ajatella kaksi ulotteinen kone, joka on ollut venytetty osaksi kolmas ulottuvuus.,

tässä tilanteessa voimme valita koordinaatit, jotka muodostavat suorakulmaisen ruudukon, kun heijastetaan vaakatasossa, kuitenkin, että henkilö asuu pinta sitten jotkut ruudukossa näkyy suurempi alue kuin toiset ja ruudukko ei näyttäisi olevan samansuuntainen. Ei ole olemassa kaksiulotteista koordinaatistoa, joka säilyttäisi rinnakkaiset linjat, kulmat ja alueet samanaikaisesti.,
samanlainen esimerkki on yrittää kartoittaa maapallon pinnan, voimme käyttää leveyttä ja pituutta linjat, mutta pituutta linjat päästä lähemmäksi lähempänä napoja.
näissä tapauksissa voisimme työn kannalta 3-ulotteinen koordinoi ja se on lähestymistapa, otamme joidenkin ei-Euclidean eriytyneistä. On usein mahdollista upottaa tietty geometria korkeampiulotteiseen geometriaan, jotta siitä tulisi Euklidisempi.,
joskus on niin, että kun katsomme geometria suuressa mittakaavassa, että se on ei-Euclidean, mutta jos katsomme sitä pienemmässä ja pienemmässä mittakaavassa niin, että se vastaa a Euklidinen geometria. Voit tehdä tämän meidän täytyy löytää koordinaatistossa, jossa kulmat säilyvät jokaisessa pisteessä, että on, vaaka-ja pystysuora koordinaatti linjat täytyy aina leikkaavat 90°, vaikka linjat voi olla suora. Tämä tunnetaan konformigeometriana. Tämäntyyppisessä geometriassa voimme ainakin määritellä paikallisen koordinaatiston.,
tähän Liittyy se, onko geometria voidaan eriyttää ja integroitu edellytys tälle on se, että se on hyvin käyttäytyviä ja ei ole mitään äkkinäisiä hyppyjä jne. Jotkin geometriat ja koordinaattijärjestelmät voivat olla paikoin hyvin käyttäytyviä, mutta niissä on singulariteetteja jne.
keskustelua kaarevuuden mittaamisesta katso tämä sivu.
Matemaattinen Notaatio
Miten me käsitellä geometriat, joissa emme voi käyttää kaikkia sääntöjä, joita sovelletaan euklidinen geometria?,
yksi lähestymistapa on käyttää tensor-merkintää, tämä tarjoaa yleissopimuksia ja merkintää, jotka auttavat meitä vaihtamaan eri koordinaattijärjestelmien välillä. Mihin tahansa pisteeseen paikallinen ortogonaalinen koordinaatisto voidaan määritellä käyttämällä pohjavektoreita, jotka ovat koordinaattilinjojen tangentteja.,Moninaiset
katso tämä sivu.
Suhde Hyperbolinen ja Minkowski Geometriat
| Minkowski Geometria | Hyperbolinen Geometria | |
| kohta | tapahtuma aika-avaruus – | hiukkanen tasaisessa liikkeessä |
| etäisyys kahden pisteen välillä | aika-avaruuden intervalli kahden tapahtuman välillä | suhteellinen nopeus kahden tällaisia hiukkasia |
Termejä
Täällä me tarkastelemme käsitteitä, kuten geometrian, tilat, mallit, ennusteet ja muunnoksia., Sen melko vaikeaa, kun me alamme käsitellä ei-Euclidean eriytyneistä koska käytämme vastaavia termejä, joita olemme tottuneet perinteisen Euklidisen avaruuden mutta ehdot voi olla hieman eri ominaisuuksia.,kokeile
Elliptinen Geometria
Mallit
Esimerkkejä ovat:
- Ylä-puoli-kone malli
- Poincare disc-malli
- Projektiivinen malli
- Konforminen malli
Ennusteet
Stereograafinen Projektio,
Muuttaa
Invariant
Esimerkkejä ovat:
- Möbius-Muunnos
- Lorentz-Muunnos
Parallel Postulate
Jos otamme pois rinnakkaisen postulate alkaen Euclidean Avaruudessa.,
Tämä johtaa:
- parallel postulate on false
- kulmat kolmion eivät lisää π
- jonkin muodon tietyn koon, ei yleensä ole samanlainen muoto, suurempi koko.,ctive
conformal (Poincaré-levy ) suorat linjat – geodesics segmenttien piireissä kulma säilyttää enemmän sisäinen kulmat, kolmio π-(α+β+γ)=CΔ etäisyys kahden pisteen välillä kanssa