Finite automata voi olla lähdöt vastaa jokainen siirtyminen. On olemassa kahdenlaisia finite state machines, joka tuottaa lähtö −
- Jauhoinen Kone
- Moore kone
Jauhoinen Kone
Jauhoinen Kone on FSM, joiden tuotanto riippuu nykytilasta sekä nykyisen tulo.,
Se voi olla kuvattu 6 monikko (Q, Å -, O -, δ, X, q0), jossa −
-
Q on äärellinen joukko valtioita.
-
∑ on äärellinen joukko symboleja kutsutaan input alphabet.
-
O on äärellinen joukko symboleja kutsutaan lähtö aakkoset.
-
δ on input siirtyminen toiminto, jossa δ: Q × ∑ → Q,
-
X on tuotannon siirtyminen toiminto, jossa X: Q × ∑ → O
-
q0 on alkutila, josta kaikki tulo on käsitelty (q0 ∈ Q).,b424468″>
Output
The state diagram of the above Mealy Machine is −
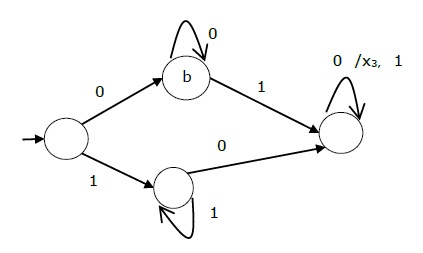
Moore Machine
Moore machine is an FSM whose outputs depend on only the present state.,
Moore kone voidaan kuvata 6 monikko (Q, Å -, O -, δ, X, q0), jossa −
-
Q on äärellinen joukko valtioita.
-
∑ on äärellinen joukko symboleja kutsutaan input alphabet.
-
O on äärellinen joukko symboleja kutsutaan lähtö aakkoset.
-
δ on input siirtyminen toiminto, jossa δ: Q × ∑ → Q,
-
X on tuotannon siirtyminen toiminto, jossa X: Q → O
-
q0 on alkutila, josta kaikki tulo on käsitelty (q0 ∈ Q).,iv>
Present state Next State Output Input = 0 Input = 1 → a b c x2 b b d x1 c c d x2 d d d x3 The state diagram of the above Moore Machine is −
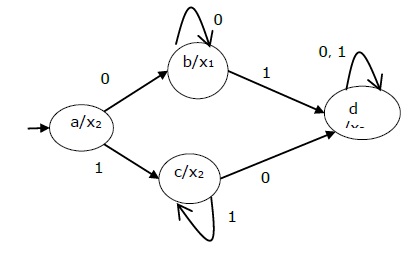
Mealy Machine vs., Moore Machine
seuraava taulukko korostaa kohtia, jotka erottavat Mealy-koneen Mooren koneesta.
Jauhoinen Kone Moore Kone Ulostulo riippuu sekä siitä esittää valtion ja läsnä input Ulostulo riippuu vain, kun läsnä tilassa. yleensä sillä on vähemmän osavaltioita kuin Moore Machinella. yleensä sillä on enemmän tiloja kuin Mealy Machinella., arvo lähtö-toiminto on funktio siirtymiä ja muutoksia, kun tulo logiikka nykytila on valmis. lähtöfunktion arvo on nykyisen tilan funktio ja kellon reunojen muutokset aina, kun tilan muutoksia tapahtuu. Mealy-koneet reagoivat tuloihin nopeammin. Ne reagoivat yleensä samalla kellosyklillä. Mooren koneissa tarvitaan enemmän logiikkaa ulostulojen purkamiseen, jolloin piiriviiveet lisääntyvät. Ne reagoivat yleensä yhden kellosyklin myöhemmin., Moore Kone Jauhoinen Kone
Algoritmi 4
Input − Moore Kone,
Lähtö − Jauhoinen Kone,
Vaihe 1 − Ota tyhjä Jauhoinen Kone siirtyminen taulukon muodossa.
Vaihe 2 − kopioi kaikki Moore Machine transition valtiot tähän taulukkomuotoon.
Vaihe 3 − Tarkista nykyiset valtiot ja niiden vastaavat lähdöt Moore Kone valtion pöydän; jos valtion Qi lähtö on m, kopioi se lähtö sarakkeet Jauhoinen Kone valtio taulukko missä Qi ilmestyy ensi tilassa.,der the following Moore machine −
Present State Next State Output a = 0 a = 1 → a d b 1 b a d 0 c c c 0 d b a 1 Now we apply Algorithm 4 to convert it to Mealy Machine.,8″>
Output
Mealy Machine to Moore Machine
Algorithm 5
Input − Mealy Machine
Output − Moore Machine
Step 1 − Calculate the number of different outputs for each state (Qi) that are available in the state table of the Mealy machine.,
Vaihe 2 − Jos kaikki Qi: n lähdöt ovat samat, Kopioi tila Qi. Jos sillä on n erilliset lähdöt, break Qi osaksi n valtiot Qin jossa n = 0, 1, 2…….
Vaihe 3 − Jos lähtö alkutila on 1, aseta uusi alkutila alusta, joka antaa 0-teholla.,b424468″>
Output
Here, states ‘a’ and ‘d’ give only 1 and 0 outputs respectively, so we retain states ‘a’ and ‘d’., Mutta valtiot ” b ” ja ” c ” tuottavat erilaisia tuotoksia (1 ja 0). Joten, jaamme b b0, b1 ja c tulee c0, c1.,”>
Output