poikkileikkaukset

Ominaisuudet-Alueet

Centroid

centroid muoto edustaa kohtaa, josta alueen osa on tasaisesti jakautunut. Jos alue on kaksin verroin symmetrinen kahden ortogonaalisen akselin suhteen, keskipiste sijaitsee näiden akselien leikkauspisteessä. Jos alue on symmetrinen noin vain yhden akselin, sitten centroid piilee jossain vaiheessa, että akseli (toinen koordinaatti on laskettava)., Jos tarkka sijainti centroid ei voi määrittää tarkastuksen, se voidaan laskea:

missä dA edustaa alueen äärettömän pieni elementti, on kokonaispinta-ala poikkileikkauksen, ja x ja y ovat koordinaatit elementti dA akseliin nähden etua.,

yhteisten poikkileikkausten centroidaalipaikat on dokumentoitu hyvin, joten sijaintia ei yleensä tarvitse laskea yllä olevilla yhtälöillä., perus muotoja, joiden centroidal sijainnit ovat tiedossa suhteen jonkin vertailukohdan, sitten centroidal sijainti composite poikkileikkaus voidaan laskea seuraavasti:

missä xc,i ja yc,en ovat suorakaiteen koordinaatit centroidal sijainti i jakso suhteessa kiintopisteeseen, ja Ai on alue i osassa.,

Centroidal Etäisyys

centroidal etäisyys, c on etäisyys centroid poikkileikkaus äärimmilleen kuitua., Se centroidal etäisyys y-suunnassa suorakulmainen poikkileikkaus on esitetty alla olevassa kuvassa:

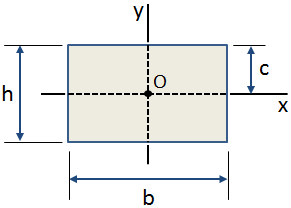
Yleisiä käyttötarkoituksia centroidal etäisyys ovat:

• enimmäismäärän laskennassa taivutusjännitys poikkileikkaus
• arvon laskennassa on ensimmäinen hetki alueella, Q, edellä kohta poikkileikkaus määrittää leikkausjännitys siinä vaiheessa

Ensimmäinen Hetki Alueella

ensimmäinen hetki-ala suhteessa akselin korko lasketaan seuraavasti:

Qx = ∫ y dA

Aj = ∫ x dA

Qx on ensimmäinen hetki noin x-akselin ja Aj on ensimmäinen hetki siitä, että y-akselilla.,Jos alue koostuu kokoelma perusmuotoja, joiden centroidal sijainnit ovat tiedossa akseliin nähden etua, sitten ensimmäinen hetki komposiitti-ala voidaan laskea seuraavasti:

Huomaa, että ensimmäinen hetki alueella käytetään laskettaessa centroid poikkileikkaus osalta joitakin alkuperä (kuten edellä)., Ensimmäistä hetkeä käytetään myös laskettaessa leikkausjännityksen arvoa tietyssä kohdassa poikkileikkauksessa. Tässä tapauksessa, ensimmäinen hetki, lasketaan alue, joka muodostaa pienemmän osan poikkileikkaus, jossa alue rajoittuu kiinnostava ja äärimmäisen kuitua (ylhäältä tai alhaalta) poikkileikkaus. Ensimmäinen hetki lasketaan poikkileikkauksen keskipisteen läpi kulkevasta akselista.,

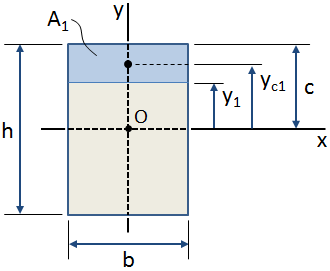
yllä olevassa kuvassa, tummennetut sininen alue on alue kiinnostaa sisällä yleinen poikkileikkaus.,nt tämän alueen suhteen x-akselin (joka kulkee poikkileikkauksen centroid, kohta O kuvassa yllä) lasketaan seuraavasti:

Jos centroidal sijainti kiinnostava alue on tiedossa, sitten ensimmäinen hetki alueella akseliin nähden voidaan laskea seuraavasti (katso kuva yllä):

olisi huomattava, että ensimmäinen hetki-ala on positiivinen tai negatiivinen riippuen asemasta asema-alueen osalta akseli kiinnostaa., Siksi koko poikkileikkauksen alueen ensimmäinen hetki suhteessa omaan centroidiinsa on nolla.

Alueen Hitausmomentti

toinen hetki alueella, joka tunnetaan paremmin nimellä hitausmomentti I, poikkileikkaus on maininta rakenneosan kykyä vastustaa taivutusta.,(Huomautus 1) Ix ja Iy ovat hetkiä, inertia noin x – ja y – akselit, vastaavasti, ja ne lasketaan seuraavasti:

Ix = ∫ y 2 dA

Bb = ∫ x2 dA

missä x ja y ovat koordinaatit elementti dA akseliin nähden etua.

yleisimmin hetkiä hitausmomentti lasketaan suhteessa kohta on centroid. Tällöin niistä käytetään nimitystä inertiamomentit, ja ne merkitään Icx: ksi X-akselin suhteen ja jäiseksi y-akselin inertialle.,

yhteisten poikkileikkausten inertiahetket on dokumentoitu hyvin, joten niitä ei yleensä tarvitse laskea yllä olevilla yhtälöillä. Tämän sivun lopussa on useita yhteisiä poikkileikkauksia.

Mikäli poikkileikkaus koostuu kokoelma perusmuotoja, joiden centroids ovat kohdakkain, niin hitausmomentti komposiitti-osio on yksinkertaisesti summa yksittäisiä hetkiä hitaus. Esimerkkinä tästä on laatikko palkki, joka koostuu kahdesta suorakaiteen kohdissa, kuten alla., Tässä tapauksessa, ulompi osa on ”positiivinen alue” ja sisempi osa on ”negatiivinen alue,” niin komposiitti hitausmomentti on vähennyslasku hitausmomentti sisemmän osan ulko-osan.

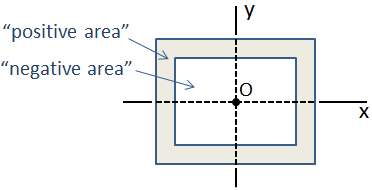
kun kyseessä on monimutkaisempi composite poikkileikkaus, jossa centroidal sijainnit eivät ole kohdakkain, hitausmomentti voidaan laskea käyttäen parallel-axis theorem.

on tärkeää, ettei alueen hitausmomenttia sekoiteta kiinteän kappaleen inertiamomenttiin., Alueen hitausmomentti osoittaa poikkileikkauksen kestävyys taivutus, kun taas massa hitausmomentti osoittaa kehon vastustuskykyä kierto.,

Parallel-Axis Theorem

Jos hitausmomentti poikkileikkauksen noin centroidal akseli on tiedossa, niin parallel-axis theorem voidaan laskea hitausmomentti mitään rinnakkainen akseli:

missä Ic on hitausmomentti noin centroidal akseli, d on etäisyys centroidal akselin ja samanaikaisesti akseli, ja on alueen poikkileikkaus.,

Mikäli poikkileikkaus koostuu kokoelma perusmuotoja, joiden centroidal hetkiä hitausmomentti tunnetaan yhdessä etäisyydet centroids jonkin vertailukohdan, sitten parallel-axis theorem voidaan laskea hitausmomentti composite poikkileikkaus.

esimerkiksi, I-Palkki voidaan approksimoida 3 suorakulmioita, kuten alla. Koska tämä komposiitti-osiossa on symmetrinen sekä x – ja y – akselit, centroid, osa voi sijaita tarkastuksen risteyksessä nuo akselit. Centroid sijaitsee origossa, O, kuvassa.,

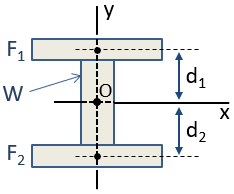
hitausmomentti composite-osiossa voidaan laskea käyttämällä parallel-axis theorem. Jakson inertiamomentti x-akselin suhteen, Icx, lasketaan seuraavasti:

missä Icx ehdot ovat hetkiä inertia yksittäisiä osia omasta centroids suunta x-akselin, d-ehdot ovat etäisyydet, yksittäisen osan centroids komposiitti kohta centroid, ja ehdot ovat alueita yksittäiset osat. Koska centroid§: N ja centroid, komposiitti-osiossa ovat päällekkäisiä, d on nolla, että jakso ja niin ei ole Ad2 aikavälillä.,

on tärkeää huomata, seuraus parallel-axis theorem, että yksittäinen jakso siirtyy kauemmaksi centroid, komposiitti kohta, vaikutus, että osa yhdistetyn jakson on hitausmomentti kasvaa kertoimella d2. Siksi, jos tarkoitus on lisätä hitausmomentti osa tietystä akseli, se on tehokkain paikantaa alue niin kaukana, että akselia kuin mahdollista. Tämä selittää I-säteen muodon., Laipat ovat ensisijaisia tukijoita hitausmomentti, ja web palvelee erilliset laipat päässä taivutus-akselilla. Web ei tarvitsee säilyttää joitakin paksuus kuitenkin välttää nurjahdus ja koska web-vie merkittävän osan leikkausjännitys jaksossa.

Polaarinen Hitausmomentti

polar hitausmomentti I, poikkileikkaus on maininta rakenneosan kyky vastustaa vääntö siitä akselin ympäri, joka on kohtisuorassa osa., Polaarinen hitausmomentti osio suhteessa akselin ympäri voidaan laskea seuraavasti:

missä x ja y ovat koordinaatit elementti dA akseliin nähden etua, ja r on etäisyys elementti dA ja akselin kiinnostusta.,

Vaikka polaarinen hitausmomentti voidaan laskea käyttämällä yhtälöä edellä, se on yleensä helpompi laskea sen käyttämällä kohtisuorassa akselin lause, jossa todetaan, että polaarinen hitausmomentti ala on summa hetkiä inertia noin kaksi kohtisuoraa akselia, jotka kulkevat akselin etu:

yleisimmin, akselin kiinnostusta kulkee centroid, poikkileikkaus.,

taivutusvastus

suurin taivutusjännitys palkki lasketaan σb = Mc / Ic, missä c on etäisyys neutraali akseli äärimmilleen kuitua, Icis, että centroidal hitausmomentti ja M on taivutusmomentti. Taivutusvastus yhdistää c ja Ic-termien taivutus stressiä yhtälö:

Käyttämällä taivutusvastusta taivutusjännitys on laskettu yhtä σb = M / S. hyödyllisyys taivutusvastus on, että se luonnehtii taivutus vastus poikkileikkaus yhden aikavälin., Tämä mahdollistaa optimoinnin säteen poikkileikkaus vastustaa taivutus maksimoimalla yhden parametrin.

Säde Kiertosäde

säde kiertosäde edustaa etäisyys kohta on centroid, jossa kaikki alueen voitaisiin keskittää ilman mitään vaikutusta hitausmomentti.,>

A polar radius of gyration can also be calculated for problems involving torsion about a centroidal axis:

The rectangular radii of gyration can also be used to calculate the polar radius of gyration:

Ominaisuudet Yhteisen poikkileikkaukset

alla Oleva taulukko antaa ominaisuuksia common poikkileikkauksia. Laajemmat taulukot löytyvät listatuista viittauksista.

ominaisuudet laskettu taulukossa ovat alue, centroidal hitausmomentti, taivutusvastus, ja säde kiertosäde.,

Huomautuksia

Huomautus 1: Taipuma Palkin

taipuma palkin alle taivutus määräytyy hitausmomentti poikkipinta, pituus palkki, ja kimmokerroin materiaali. Lisätietoja annetaan tässä keskustelussa palkki taipuma.