Ratkaisemaan Yhtälöitä Numeerisesti

Löytää Kaikki Juuret polynomifunktion Toiminta

Käyttö vpasolve löytää kaikki ratkaisut funktio f(x)=6×7-2 x 6+3×3-8.

syms f(x)f(x) = 6*x^7-2*x^6+3*x^3-8;sol = vpasolve(f)

vpasolve palaa seitsemän juuret toiminto, kuten odotettua, koska toiminto on polynomin aste seitsemän.,

Etsi Nollia, on Nonpolynomial Toiminto Käyttämällä Search-Alueet ja lähtökohdat

tontti funktio f(x)=e(x/7)cos(2x) paljastaa määräajoin nollia, yhä rinteillä nolla pistettä, kun x kasvaa.

syms xh = fplot(exp(x/7)*cos(2*x),);grid on

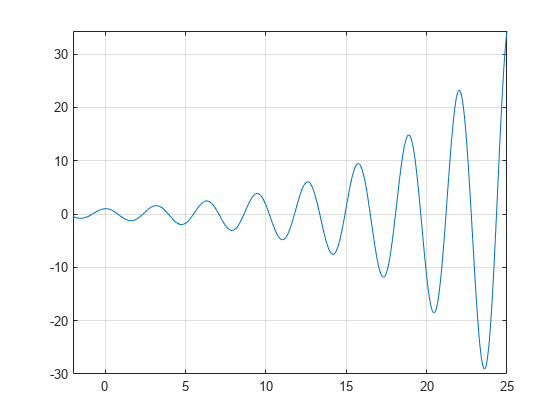
Käyttö vpasolve löytää nolla toiminto f. Huomaa, että vpasolve palauttaa vain yhden nonpolynomiaaliyhtälön ratkaisun, vaikka ratkaisuja olisi useita., On repeated calls, vpasolve returns the same result.

f = exp(x/7)*cos(2*x);for k = 1:3 vpasolve(f,x)end

ans = -7.0685834705770347865409476123789-vpa('7.0685834705770347865409476123789')

ans = -7.0685834705770347865409476123789-vpa('7.0685834705770347865409476123789')

ans = -7.0685834705770347865409476123789-vpa('7.0685834705770347865409476123789')

To find multiple solutions, set the option 'Random' to true. This makes vpasolve choose starting points randomly., For information on the algorithm that chooses random starting points, see Algorithms on the vpasolve page.

for k = 1:3 vpasolve(f,x,'Random',true)end

ans = -226.98006922186256147892598444194-vpa('226.98006922186256147892598444194')

ans = 98.174770424681038701957605727484vpa('98.174770424681038701957605727484')

ans = 52.621676947629036744249276669932vpa('52.621676947629036744249276669932')

To find a zero close to x=10, set the starting point to 10.,

vpasolve(f,x,10)

ans = 10.210176124166828025003590995658vpa('10.210176124166828025003590995658')

löytää nolla majoitusliike, x=1000, aseta lähtökohta 1000.

vpasolve(f,x,1000)

ans = 999.8118620049516981407362567287vpa('999.8118620049516981407362567287')

löytää nolla välillä 15≤x≤25, määritä haun alue .,

vpasolve(f,x,)

ans = 21.205750411731104359622842837137vpa('21.205750411731104359622842837137')

löytää useita nollia alue , et voi soittaa vpasolve toistuvasti, koska se palauttaa saman tuloksen jokaisen puhelun, kuten aiemmin on esitetty. Sen sijaan, aseta hakualue ja asettaa 'Random' ja true.,

for k = 1:3 vpasolve(f,x,,'Random',true)end

ans = 21.205750411731104359622842837137vpa('21.205750411731104359622842837137')

ans = 21.205750411731104359622842837137vpa('21.205750411731104359622842837137')

ans = 16.493361431346414501928877762217vpa('16.493361431346414501928877762217')

Koska 'Random' valitsee lähtökohdat satunnaisesti, sama ratkaisu saattaa löytyä peräkkäiset puhelut.,

Löytää Kaikki Nollia Määritelty Haku Alue

Luo toiminto findzeros järjestelmällisesti löytää kaikki nollat f tietyssä search-alue, tietyn virhe toleranssi. Funktio alkaa tulonhakualueella ja kutsuu vpasolve etsimään Nollaa. Sitten, se jakaa hakualue kahteen noin nolla arvo ja kutsuu itseään rekursiivisesti kanssa uusi haku vaihtelee panoksina löytää enemmän nollia.

funktio selitetään osioittain tässä.,

ilmoittaa funktion kolmella syötteellä ja yhdellä ulostulolla. Ensimmäinen syöttö on toiminto, toinen tulo on alue, ja valinnainen kolmas input avulla voit määrittää virheen välillä nolla ja korkeampi ja alempi rajat syntyvät siitä.

function sol = findzeros(f,range,err)

Jos et määritä valinnainen argumentti virhe toleranssi, findzeros asetetaan err ja 0.001.

if nargin < 2 err = 1e-3;end

Löytää nolla, etsi-alueella käyttäen vpasolve.,

sol = vpasolve(f,range);

– Jos vpasolve ei löydä nolla, poistu.

if(isempty(sol)) return

– Jos vpasolve löytää nolla, jakaa hakualue kahteen haku vaihtelee yli ja alle nollan.

else lowLimit = sol-err; highLimit = sol+err;

Soittaa findzeros pienempi hakualue. Jos findzeros palauttaa nollat, kopioi arvot ratkaisurivistöön ja lajittele ne.

 temp = findzeros(f,,1); if ~isempty(temp) sol = sort(); end

Soittaa findzeros suurempi hakualue., Jos findzeros palauttaa nollat, kopioi arvot ratkaisurivistöön ja lajittele ne.

 temp = findzeros(f,,1); if ~isempty(temp) sol = sort(); end returnendend

koko toiminto findzeros on seuraava. Tallenna tämä funktio nimellä findzeros.m nykyiseen kansioon.

syms f(x)f(x) = exp(x/7)*cos(2*x);sol = findzeros(f,)'

Saada Ratkaisuja Mielivaltaisen Tarkkuuden

Käyttö digits asettaa tarkkuus ratkaisut palautetaan vpasolve., Oletuksena vpasolve palauttaa ratkaisut 32 merkitsevän luvun tarkkuudella.

f = exp(x/7)*cos(2*x);vpasolve(f)

ans = -7.0685834705770347865409476123789-vpa('7.0685834705770347865409476123789')

Käyttö digits lisätä tarkkuus 64 merkittäviä lukuja. Kun muokkaat digits, varmista, että tallennat sen nykyisen arvon niin, että voit palauttaa sen.,

digitsOld = digits;digits(64)vpasolve(f)

ans = -7.068583470577034786540947612378881489443631148593988097193625333-vpa('7.068583470577034786540947612378881489443631148593988097193625333')

Seuraava, muuttaa tarkkuus ratkaisuja 16 merkitsevän numeron tarkkuudella.

digits(16)

Ratkaista Monimuuttuja Yhtälöitä Käyttäen Search-Alueet

Harkitse seuraavia järjestelmän yhtälöt.

juoni yhtälöt 0≤x≤2, 5 ja 0≤x≤2.5 osoittaa, että kolme pinnat leikkaavat kaksi pistettä., Hahmottaaksesi juonen paremmin, käytä view. Mittakaavassa värikartan arvot, käytä caxis.

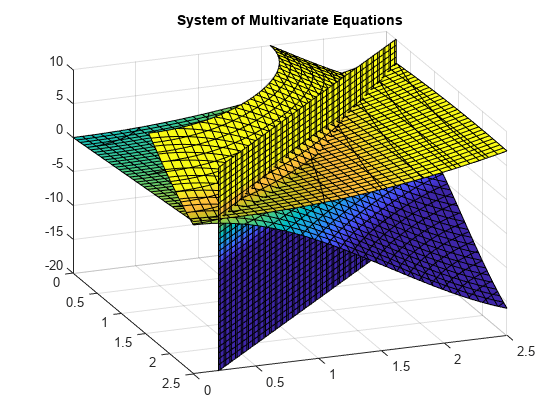
Käyttö vpasolve löytää kohta, jossa pinnat leikkaavat. Funktio vpasolve palauttaa rakenteen. Käyttää x-, y ja z-arvot ratkaisu, indeksi rakenteeseen.,

sol = vpasolve(equations);

etsiä alueen ratkaisu tilaa, määritä haku vaihtelee muuttujia. Jos määrität vaihtelee 0≤x≤1.5 ja 1.5≤y≤2.5, sitten vpasolve toiminto etsii rajoittuu alue näytetään.

Käyttö vpasolve löytää ratkaisu tähän search-alue. Jos haluat jättää pois z: n hakualueen, aseta kolmas hakualue .,

vars = ;range = ;sol = vpasolve(equations, vars, range);

löytää useita ratkaisuja, aseta 'Random' mahdollisuus true. Tämä saa vpasolve käyttämään satunnaisia lähtökohtia peräkkäisillä juoksuilla. 'Random' vaihtoehto voi olla käyttää yhdessä etsiä vaihtelee tekemään vpasolve käyttää random lähtökohdat sisällä hakualue. Koska 'Random' valitsee lähtökohdat satunnaisesti, sama ratkaisu saattaa löytyä peräkkäiset puhelut., Soitavpasolve toistuvasti varmistaaksesi, että löydät molemmat ratkaisut.

piirtää yhtälöt. Päällekkäin ratkaisuja, kuten scatter tontti pistettä keltainen X markkereita käyttäen scatter3. Havainnollistaa juonta paremmin tekemällä kahdesta pinnasta läpinäkyvät alpha. Asteikko värikartan juoni arvoja käyttäen caxis, ja muuttaa näkökulmasta käyttäen view.

vpasolve löytää ratkaisuja risteyksessä pinnat muodostetaan yhtälöt, kuten on esitetty.,

Lastly, restore the old value of digits for further calculations.

digits(digitsOld)