Sisältö
Vakio kiihtyvyys
Olemme kaikki tietoisia siitä, että auton nopeutuu, kun panemme jalka alas kaasupoljin. Hiukkasen nopeuden muutosta suhteessa aikaan kutsutaan sen kiihtyvyydeksi. Jos hiukkasen nopeus muuttuu vakionopeudella, tätä nopeutta kutsutaan vakionopeudeksi.,
esimerkiksi, jos nopeus hiukkanen liikkuu suoraviivaisesti muuttuu tasaisesti (jatkuva muutos) 2 m/s 5 m/s yli yhden sekunnin, sitten sen jatkuva kiihtyvyys on 3 m/s\(^2\).
Vähentää velocity
Jos hiukkanen on aluksi nopeus 6 m/s ja jatkuva kiihtyvyys \(-2\) m/s\(^2\), niin:
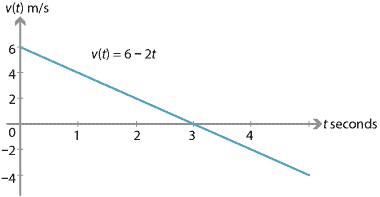
kolmen ensimmäisen sekunnin, hiukkasen nopeus on laskussa (hiukkanen on hidastumassa). Kolmen sekunnin kuluttua hiukkanen on hetkellisesti levossa., Kolmen sekunnin kuluttua, nopeus on edelleen laskussa, mutta nopeus kasvaa (hiukkanen on menossa nopeammin ja nopeammin).
Tiivistelmä
Jos oletetaan, että korko muutos nopeus (kiihtyvyys) on jatkuva, niin jatkuva kiihtyvyys on antanut
\
tarkemmin, jatkuva kiihtyvyys \(a\) on kaavasta
\
missä \(v(t_i)\) on nopeus, aika \(t_i\). Koska nopeus on vektori, samoin kiihtyvyys.,
vakio-kiihtyvyys kaavoja liikkeen suora linja
Koko tässä jaksossa, olemme pohtineet liike suorassa linjassa jatkuva kiihtyvyys. Tilanne on hyvin yleinen; esimerkiksi painovoiman vaikutuksesta liikkuva kappale kulkee jatkuvalla kiihtyvyydellä.
oletetaan, että liike alkaa, kun \(t = 0\), ja sen alustava kanta on otettu alkuperää, eli \(x(0) = 0\).,
viisi liikeyhtälöt
- \(v = u + at\)
- \(x = \dfrac{(u+v)t}{2}\)
- \(x = ut + \dfrac{1}{2}at^2\)
- \(v^2 = u^2 + 2ax\)
- \(x = vt – \dfrac{1}{2}at^2\)
Huom. Jokaisen viiden yhtälöt mukaan neljä viidestä muuttujien \(u, v, x, a, t\). Jos muuttujien kolmen arvot tunnetaan, jäljelle jäävät arvot voidaan löytää käyttämällä kahta yhtälöä.,
Perustuvat jatkuva-kiihtyvyys kaavat
ensimmäinen yhtälö liikkeen
Koska kiihtyvyys on vakio, meillä on \(a = \dfrac{v, u}{t}\). Tämä antaa ensimmäisen yhtälön liikkeen, \(v = u+\).
toinen yhtälö liikkeen
toinen yhtälö,
\
sanoo, että siirtymä saadaan kertomalla keskimääräinen alkuperäisen ja lopullisen nopeudet mennessä kulunut liikkeen aikana. Yksinkertaisemmin:
\
voimme johtaa tämän yhtälön käyttämällä sitä, että uppouma on yhtä suuri kuin allekirjoitettu alue nopeus–ajan kuvaajan alla.,
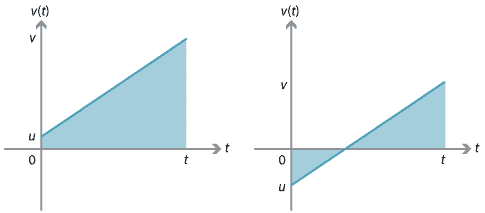
kuvaajan oikealla, siirtymä voidaan löytää tarkastelemalla kaksi kolmiota välillä kuvaajan ja \(t\)-akselilla. Yksi kolmioista on positiivinen allekirjoitettu alue ja toinen on negatiivinen allekirjoitettu alue.
hiukkasen siirtymän löytämistä nopeus–ajan kuvaajasta integroinnin avulla käsitellään tämän moduulin myöhemmässä osassa.,
kolmas yhtälö liikkeen
Korvaamalla \(v\) ensimmäinen yhtälö toiseen yhtälöön antaa
\begin{align*}x &= \dfrac{(u+v)t}{2} \\ &= \dfrac{(u+u+at)t}{2} \\ &= \dfrac{2ut+at^2}{2} \\ &= ut + \dfrac{1}{2}at^2, \end{align*}
joka on kolmas yhtälö. Niinpä \(x\) on neliö \(t\), ja siten kuvaaja \(x\) vastaan \(t\) on paraabeli.
liikkeen neljäs yhtälö
ensimmäisestä yhtälöstä meillä on \(t = \dfrac{v-u}{a}\)., Sijoittamalla tämä toiseen yhtälöön antaa
\begin{align*}x &= \dfrac{(u+v)t}{2} \\ &= \dfrac{(u+v)(v-u)}{2a} \\ &= \dfrac{v^2-u^2}{2a}. \end{align*}
Järjestämällä tehdä \(v^2\) aihe tuottaa neljäs yhtälö: \(v^2 = u^2 + 2ax\).
liikkeen viides yhtälö
ensimmäisestä yhtälöstä meillä on \(u = V-at\)., Käyttämällä toinen yhtälö, saadaan
\begin{align*}x &= \dfrac{(u+v)t}{2} \\ &= \dfrac{(v-at+v)t}{2} \\ &= \dfrac{2vt-at^2}{2} \\ &= vt-\dfrac{1}{2}at^2, \end{align*}
joka on viides yhtälö.
pystysuuntainen liike
painovoimasta johtuva liike on hyvä konteksti, jossa voidaan osoittaa vakiokiihtyvyyden kaavojen käyttö., Kuten aiemmin, meidän kaksi suuntiin pystysuora liike on ylös ja alas, ja päätös on tehtävä siitä, mikä kahteen suuntaan on positiivinen. Painovoimasta johtuva kiihtyvyys on vakio, jonka magnitudi merkitään \(g\). Seuraavassa esimerkissä otamme ylöspäin suunta olla positiivinen ja ottaa \(g = 10\) m/s\(^2\).
Harjoitus 3
mies sukeltaa ponnahduslauta, jossa hänen painopiste on aluksi 12 metriä vedenpinnan yläpuolella, ja hänen lähtönopeus on 4,9 m/s ylöspäin., Huomioon sukeltaja kuin hiukkanen, hänen painopiste, ja olettaa, että sukeltajan liike on vertikaalinen.
- Etsi sukeltajan nopeus \(t\) sekunnin jälkeen (aina veteen osuessaan).
- Etsi sukeltajan korkeus veden yläpuolella \(t\) sekunnin jälkeen (aina veteen osuessaan).
- Etsi sukeltajan maksimikorkeus vedenpinnan yläpuolella.
- Löytää aikaa ottaa sukeltaja päästä vettä.,
- Luonnos nopeus–aika-kuvaaja tämän liikkeen (ylös, kun hän osuu veteen).
- Luonnos kanta–aika kuvaajan tämän liikkeen (ylös, kun hän osuu veteen).
Edelleen käyttää liikeyhtälöt
Harjoitus 7
auto kiihtyy 0 km/h 100 km/h 10 sekunnissa, ja jatkuu 40 sekuntia 100 km/h. Kuljettaja ja sitten jarruttaa voimakkaasti lopettaa 38 metriä.
- Muunna 100 km/h, m/s.,
- Löytää vakio kiihtyvyys auton ensin 10 sekuntia m/s\(^2\).
- Etsi auton kokonaismatka metreinä.
- Löytää kiihtyvyys jarrutuksen vaihe m/s\(^2\).
- Kuinka kauan kestää, että auto pysähtyy kun jarrua on ensin sovellettu?
- piirtää nopeus–ajan kuvaajan auton liikkeelle.,
Next page – Content – Average velocity and average speed
 |
This publication is funded by the Australian Government Department of Education, Employment and Workplace Relations |
Contributors Term of use |