”Unit Circle” on ympyrä, jonka säde on 1.
koska se on niin yksinkertaista, se on hyvä tapa oppia ja puhua pituuksista ja kulmista.
keskipiste laitetaan kuvioon, jossa x-akseli ja y-akseli risteytyvät, joten saamme tämän siistin asetelman tästä.
Sini, Kosini ja Tangentti
Koska säde on 1, emme voi suoraan mitata sini, kosini ja tangentti.,
Mitä tapahtuu, kun kulma θ on 0°?
cos 0° = 1, sin 0° = 0 ja tan 0° = 0,
Mitä tapahtuu, kun θ on 90°?
cos 90° = 0, sin 90° = 1 ja tan 90° on määrittelemätön
Kokeile Itse!
Have a try!, Liikuta hiirtä nähdä, miten eri näkökulmista (radiaaneina tai astetta) vaikuttaa sini, kosini ja tangentti
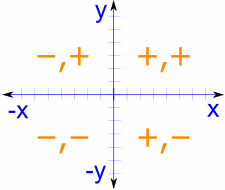
”puolta” voi olla positiivinen tai negatiivinen sääntöjen mukaan Loogiseksi koordinaatit. Tällöin sini, kosiini ja tangentti muuttuvat myös positiivisten ja negatiivisten arvojen välillä.
kokeile myös interaktiivista Yksikköympyrää.,
Pythagoras
Pythagoraan Lause sanoo, että oikeus kulma kolmion, neliön pitkä sivu on yhtä suuri kuin summa neliöiden kaksi muuta sivua:
x2 + y2 = 12
Mutta 12 on vain 1, niin:
x2 + y2 = 1
(yhtälö yksikkö ympyrä)
Myös, kun x=cos ja y=sin, saamme:
(cos(θ))2 + (sin(θ))2 = 1
hyödyllinen ”identiteetti”
Tärkeää Kulmat: 30°, 45° ja 60°
Sinun pitäisi yrittää muistaa, sin, cos ja tan kulmat 30°, 45° ja 60°.,
kyllä, Kyllä, se on tuskaa täytyy muistaa asioita, mutta se tekee elämästä helpompaa, kun tiedät ne, ei vain tentit, mutta muina aikoina, kun sinun täytyy tehdä nopeita arvioita, jne.
nämä arvot kannattaa muistaa!,id=”0f47f3223b”>
What about tan?,
No, tan = sin/cos, jotta voimme laskea sen näin:
tan(30°) =sin(30°)cos(30°) = 1/2√3/2 = 1√3 = √33 *
tan(45°) =sin(45°)cos(45°) = √2/2√2/2 = 1
tan(60°) =sin(60°), koska(60°) = √3/21/2 = √3
* Huomaa: kirjoittaminen 1√3 voi maksaa jälkiä (ks Järkevä Nimittäjät), joten sen sijaan käyttää √33
Nopea Luonnos
Toinen tapa auttaa sinua muistamaan, 30° ja 60° on tehdä nopea luonnos:
| Piirrä kolmio, jonka sivujen pituudet 2 | 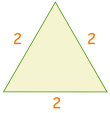 |
|
|
Leikkaa kahtia.,div id=”56c966b492″> Esimerkki: sin(30°)Sini: sohcahtoa sini on päinvastainen jaettuna hypotenuusan
sin(30°) = oppositehypotenuse = 12
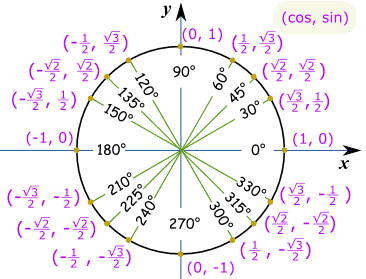
Koko Ympyräkoko ympyrä tarvitsemme arvoja jokaisen quadrant, oikea plus tai miinus-merkki kohti Suorakulmaiset Koordinaatit: Huomaa, että koska on ensimmäinen ja synti on toinen, niin se menee (cos, synti):
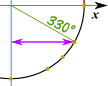
Tallenna PDF-tiedostona Esimerkki: Mitä on cos(330°) ?,
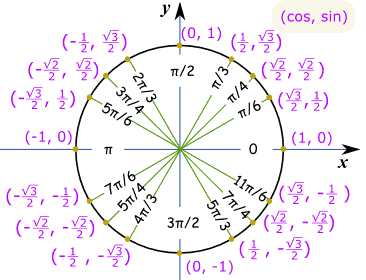
Tehdä luonnos, kuten tämä, ja voimme nähdä, se on ”pitkä” arvo: √32 Ja tämä on sama Yksikkö Ympyrä radiaaneina.
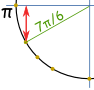
Esimerkki: Mikä on syntiä(7π/6) ?
Ajattele ”7π/6 = π + π/6”, sitten tehdä luonnos. Voimme nähdä, se on negatiivinen ja on ”lyhyt” arvo: −½ |