Il “Cerchio unitario” è un cerchio con un raggio di 1.
Essendo così semplice, è un ottimo modo per imparare e parlare di lunghezze e angoli.
Il centro è messo su un grafico in cui l’asse x e l’asse y si incrociano, quindi otteniamo questa disposizione ordinata qui.
Seno, coseno e tangente
Poiché il raggio è 1, possiamo misurare direttamente seno, coseno e tangente.,

Cosa succede quando l’angolo, θ, è 0°?
cos 0°= 1, sin 0° = 0 e tan 0° = 0

Cosa succede quando θ è 90°?
cos 90° = 0, sin 90° = 1 e tan 90 ° non è definito
Prova tu stesso!
Prova!, Muovi il mouse per vedere come diversi angoli (in radianti o gradi) influenzano seno, coseno e tangente
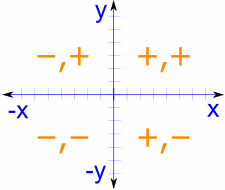
I “lati” possono essere positivi o negativi secondo le regole delle coordinate cartesiane. Questo fa sì che anche il seno, il coseno e la tangente cambino tra valori positivi e negativi.
Prova anche il Cerchio unitario interattivo.,
Pitagora
il Teorema di Pitagora dice che per un ad angolo retto del triangolo, il quadrato di un lato è uguale alla somma dei quadrati degli altri due lati:
x2 + y2 = 12
Ma il 12 è solo 1, quindi:
x2 + y2 = 1
(l’equazione del cerchio unitario)
Inoltre, dato che x=cos y=sin, si ottiene:
(cos(θ))2 + (sin(θ))2 = 1
un utile “identità”
Importante Angoli: 30°, 45° e 60°
Si dovrebbe cercare di ricordare sin, cos e tan per gli angoli di 30°, 45° e 60°.,
Sì, sì, è un dolore dover ricordare le cose, ma renderà la vita più facile quando le conosci, non solo negli esami, ma in altri momenti in cui devi fare stime rapide, ecc.
Questi sono i valori che dovresti ricordare!,id=”0f47f3223b”>
What about tan?,
Bene, tan = sin/cos, in modo che si può calcolare come segue:
tan(30°) =sin(30°)cos(30°) = 1/2√3/2 = 1√3 = √33 *
tan(45°) =sin(45°)cos(45°) = √2/2√2/2 = 1
tan(60°) =sin(60°)cos(60°) = √3/21/2 = √3
* Nota: la scrittura 1√3 può costare marchi (vedi Razionale Denominatori), così, invece di utilizzare √33
Rapido Schizzo
un Altro modo per aiutare a ricordare i 30° e i 60° è di fare un rapido schizzo:
| Disegnare un triangolo con lati di lunghezza di 2 | 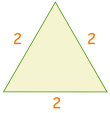 |
|
|
Tagliare a metà.,div id=”56c966b492″> Esempio: sin(30°)Sine: sohcahtoa il seno è di fronte diviso per ipotenusa
sin(30°) = oppositehypotenuse = 12
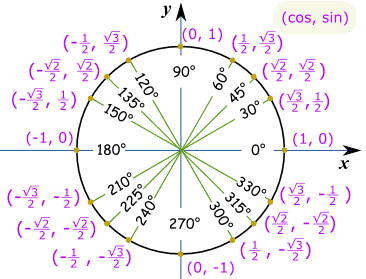
Il CerchioPer tutto il cerchio, abbiamo bisogno di valori in ogni quadrante, con il corretto segni più o meno come per Coordinate Cartesiane: Nota che cos è il primo e il peccato è la seconda, così va (cos, il peccato):
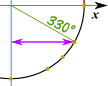
Salva come PDF Esempio: che Cosa è cos(330°) ?,
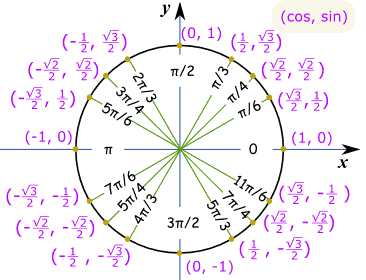
Fai uno schizzo come questo, e possiamo vedere che è il valore “lungo”: √32 E questo è lo stesso Cerchio unitario in radianti.
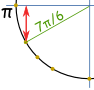
Esempio: Cos’è il peccato (7π / 6)?
Pensa “7π/6 = π + π / 6”, quindi crea uno schizzo. Possiamo quindi vedere che è negativo ed è il valore “breve”: – ½ |