Content-Accelerazione costante

Content

Accelerazione costante

Conosciamo tutti il fatto che un’auto accelera quando mettiamo il piede sull’acceleratore. Il tasso di variazione della velocità di una particella rispetto al tempo è chiamato la sua accelerazione. Se la velocità della particella cambia a una velocità costante, allora questa velocità è chiamata accelerazione costante.,

Ad esempio, se la velocità di una particella che si muove in linea retta cambia uniformemente (a una velocità di variazione costante) da 2 m/s a 5 m/s per un secondo, la sua accelerazione costante è 3 m/s\(^2\).

Velocità decrescente

Se una particella ha una velocità iniziale di 6 m/s e un’accelerazione costante di \(-2\) m/s\(^2\), allora:

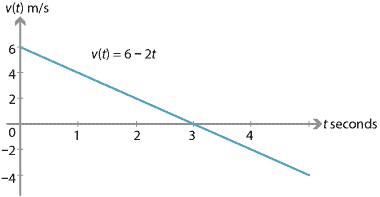
Nei primi tre secondi, la velocità della particella sta diminuendo (la particella sta rallentando). A tre secondi, la particella è momentaneamente a riposo., Dopo tre secondi, la velocità sta ancora diminuendo, ma la velocità sta aumentando (la particella sta andando sempre più veloce).

Sommario

Se si assume che il tasso di variazione della velocità (accelerazione) è una costante, la costante accelerazione è data da

\

Più precisamente, l’accelerazione costante \(a\) è data dalla formula

\

dove \(v(t_i)\) è la velocità al tempo \(t_i\). Poiché la velocità è un vettore, lo è anche l’accelerazione.,

Le formule di accelerazione costante per il movimento in linea retta

In tutta questa sezione, abbiamo considerato il movimento in linea retta con accelerazione costante. Questa situazione è molto comune; ad esempio, un corpo che si muove sotto l’influenza della gravità viaggia con un’accelerazione costante.

Si presume che il movimento inizi quando \(t = 0\) e che la posizione iniziale sia presa come origine, cioè \(x(0) = 0\).,

cinque equazioni del moto

1. \(v = u + a\)
2. \(x = \dfrac{(u+v)t}{2}\)
3. \(x = ut + \dfrac{1}{2}a^2\)
4. \(v^2 = u^2 + 2ax\)
5. \(x = vt – \dfrac{1}{2}a^2\)

Nota. Ciascuna delle cinque equazioni coinvolge quattro delle cinque variabili \(u, v, x, a, t\). Se i valori di tre delle variabili sono noti, i valori rimanenti possono essere trovati utilizzando due delle equazioni.,

Derivando le formule di accelerazione costante

La prima equazione del moto

Poiché l’accelerazione è costante, abbiamo \(a = \dfrac{v-u}{t}\). Questo dà la prima equazione del moto, \(v = u + at\).

La seconda equazione del moto

La seconda equazione,

\

dice che lo spostamento si ottiene moltiplicando la media delle velocità iniziali e finali per il tempo trascorso durante il movimento. Più semplicemente:

\

Possiamo ricavare questa equazione usando il fatto che lo spostamento è uguale all’area firmata sotto il grafico velocità–tempo.,

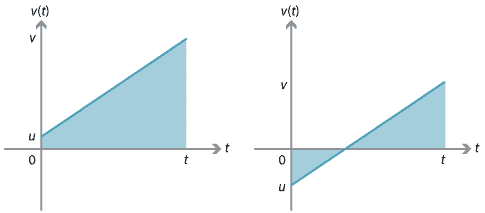
Per il grafico a destra, lo spostamento può essere trovato considerando i due triangoli tra il grafico e l’asse \(t\). Uno dei triangoli ha un’area con segno positivo e l’altro ha un’area con segno negativo.

Trovare lo spostamento di una particella dal grafico velocità–tempo usando l’integrazione sarà discusso in una sezione successiva di questo modulo.,

La terza equazione del moto

Sostituendo per \(v\) dalla prima equazione nella seconda equazione dà

\begin{align*}x &= \dfrac{(u+v)t}{2} \\ &= \dfrac{(u+u+u + a)t}{2} \\ &= \dfrac{2ut+a^2}{2} \\ &= ut + \dfrac{1}{2}a^2, \end{align*}

la terza equazione. Quindi \(x\) è un quadratico in \(t\), e quindi il grafico di \(x\) contro \(t\) è una parabola.

La quarta equazione del moto

Dalla prima equazione, abbiamo \(t = \dfrac{v-u}{a}\)., Sostituendo nella seconda equazione dà

\begin{align*}x &= \dfrac{(u+v)t}{2} \\ &= \dfrac{(u+v)(v-u)}{2a} \\ &= \dfrac{v^2-u^2}{2a}. \ end {align*}

Riorganizzando per rendere \(v^2\) il soggetto produce la quarta equazione: \(v^2 = u^2 + 2ax\).

La quinta equazione del moto

Dalla prima equazione, abbiamo \(u = v-at\)., Utilizzando la seconda equazione, si ottiene

\begin{align*}x &= \dfrac{(u+v)t}{2} \\ &= \dfrac{(v-a+t v)} {2} \\ &= \dfrac{2vt-a^2}{2} \\ &= vt-\dfrac{1}{2}a^2, \end{align*}

che è la quinta equazione.

Movimento verticale

Il movimento dovuto alla gravità è un buon contesto in cui dimostrare l’uso delle formule di accelerazione costante., Come discusso in precedenza, le nostre due direzioni in movimento verticale sono su e giù, e una decisione deve essere presa su quale delle due direzioni è positiva. L’accelerazione dovuta alla gravità è una costante, con magnitudine indicata da \ (g\). Nell’esempio seguente, prendiamo la direzione verso l’alto per essere positiva e prendiamo \(g = 10\) m/s\(^2\).

Ulteriore utilizzo delle equazioni del moto

Next page – Content – Average velocity and average speed