
La funzione delta di Dirac è una funzione introdotta nel 1930 da P. A. M. Dirac nel suo fondamentale libro sulla meccanica quantistica. Un modello fisico che visualizza una funzione delta è una distribuzione di massa di massa totale finita M-l’integrale sulla distribuzione di massa., Quando la distribuzione diventa sempre più piccola, mentre M è costante, la distribuzione di massa si restringe a una massa puntiforme, che per definizione ha un’estensione zero e tuttavia ha un integrale a valori finiti uguale alla massa totale M. Nel limite di una massa puntiforme la distribuzione diventa una funzione delta di Dirac.
Euristicamente, la funzione delta di Dirac può essere vista come un’estensione del delta di Kronecker dagli indici integrali (elementi di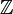 ) agli indici reali (elementi di
) agli indici reali (elementi di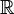 )., Nota che il delta di Kronecker agisce come un “filtro” in una sommatoria di:
)., Nota che il delta di Kronecker agisce come un “filtro” in una sommatoria di:
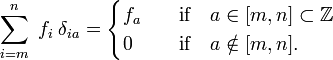
In analogia, la delta di Dirac funzione δ(x−a) è definito da (sostituire x e la somma sopra mi da un’integrazione più di x),
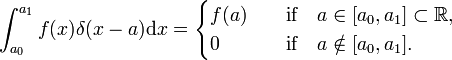
La funzione delta di Dirac non è un ordinario ben educati mappa 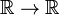 , ma una distribuzione, noto anche come un improprio o generalizzato funzione. I fisici esprimono il suo carattere speciale affermando che la funzione delta di Dirac ha senso solo come fattore in un integrando (“sotto l’integrale”)., I matematici dicono che la funzione delta è un funzionale lineare su uno spazio di funzioni di test.
, ma una distribuzione, noto anche come un improprio o generalizzato funzione. I fisici esprimono il suo carattere speciale affermando che la funzione delta di Dirac ha senso solo come fattore in un integrando (“sotto l’integrale”)., I matematici dicono che la funzione delta è un funzionale lineare su uno spazio di funzioni di test.
Contenuto
- 1 Proprietà
- 2 Delta-successione convergente
- 2.1 le funzioni di Blocco
- 2.2 Gaussiana funzioni
- 2.3 Lorentz-Cauchy funzioni
- 2.4 Sinc funzioni
- 3 Derivati della funzione delta
- 3.,1 Proprietà di derivati
- 4 Primitiva
- 5 La funzione delta di Dirac in tre dimensioni
- 6 Riferimenti
Proprietà
la Maggior parte comunemente si prende inferiore e il limite superiore nella definizione della funzione di delta uguale a 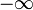 e
e 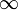 , rispettivamente. Da qui in poi questo sarà fatto.
, rispettivamente. Da qui in poi questo sarà fatto.
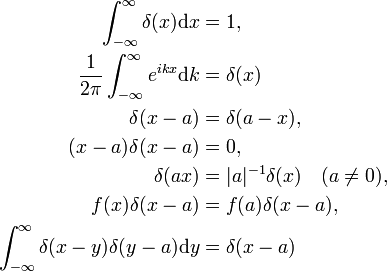
La prova del fisico di queste proprietà procede facendo sostituzioni appropriate nell’integrale e usando le regole ordinarie del calcolo integrale., La funzione delta come trasformata di Fourier della funzione unitaria f (x) = 1 (la seconda proprietà) sarà dimostrata di seguito. L’ultima proprietà è l’analogia della moltiplicazione di due identità matrici,
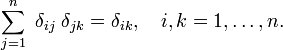
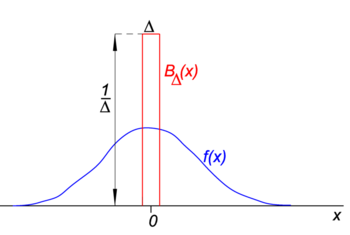
Fig. 1. Blocco (“boxcar”) funzione (rosso) volte regolare funzione f(x) (blu).
Sequenze delta-convergenti
Esistono famiglie di funzioni regolari Fa(x) di cui i membri della famiglia differiscono per il valore di un singolo parametro α., Un esempio di tale famiglia è formato dalla famiglia delle funzioni gaussiane Fa(x) = exp(−ax2), dove i diversi valori del singolo parametro α distinguono i diversi membri. Quando tutti i membri sono linearmente normalizzabili, cioè, il seguente integrale è finito indipendentemente da α,
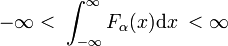
e tutti i membri raggiungono il picco intorno a x = 0, allora la famiglia può formare una sequenza delta-convergente.,
Funzioni di blocco
L’esempio più semplice di una sequenza delta-convergente è formato dalla famiglia di funzioni di blocco, caratterizzate da Δ positivo,
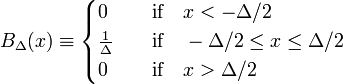
In Fig. 1 la funzione di blocco BΔ è mostrata in rosso. Evidentemente, l’area (larghezza per altezza) sotto la curva rossa è uguale all’unità, indipendentemente dal valore di Δ,
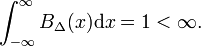
Lascia che la funzione arbitraria f (x) (blu in Fig. 1) essere continuo (senza salti) e finito nel quartiere di x = 0., Quando Δ diventa molto piccolo e la funzione di blocco molto stretta (e necessariamente molto alta perché larghezza volte altezza è costante) il prodotto f(x) BΔ(x) diventa in buona approssimazione uguale a f(0) BΔ(x). Più stretto è il blocco migliore è l’approssimazione., Quindi per Δ andando a zero,
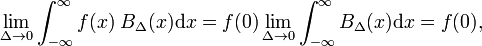
che può essere confrontata con la definizione della funzione delta,
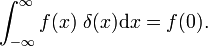
Questo dimostra che la famiglia di blocco di funzioni converge alla funzione delta di Dirac per la diminuzione del parametro Δ; la famiglia si forma un delta-convergente sequenza:
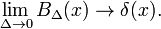
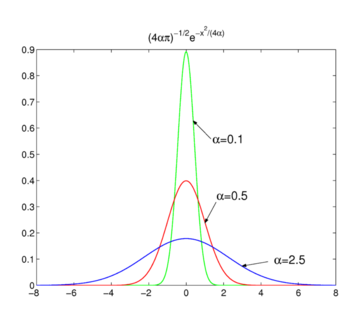
Fig. 2. Funzioni gaussiane.
Nota: Abbiamo integrato su tutto l’asse reale., Ovviamente questo non è necessario, avremmo potuto escludere le ali a valore zero della funzione di blocco e integrate solo sopra la gobba nel mezzo, da −Δ/2 a +Δ/2. Nei testi matematici, come ad esempio Ref. , questo perfezionamento nei limiti di integrazione è incluso nella definizione della sequenza delta-convergente. Cioè, è necessario che gli integrali sopra le due ali svaniscano nel limite. Poiché le sequenze delta-convergenti incontrate nelle applicazioni fisiche di solito soddisfano questa condizione, omettiamo la definizione matematica più esatta.,
Funzioni gaussiane
Considera la famiglia,
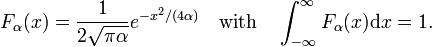
Come mostrato in Fig. 2 le funzioni raggiungono il picco intorno a x = 0 e diventano più strette per diminuire α. Quindi la famiglia di funzioni gaussiane forma una sequenza delta-convergente,
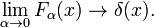
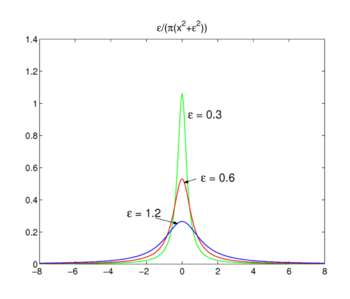
Fig. 3. Funzioni di Lorentz-Cauchy
Funzioni di Lorentz-Cauchy
La famiglia di funzioni mostrata in Fig., 3
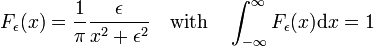
forms a delta-convergent sequence,
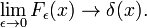
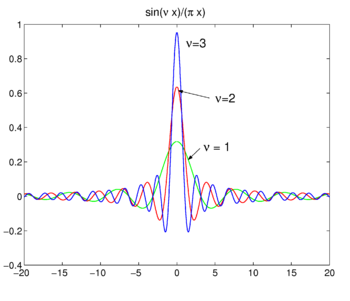
Fig. 4. Sinc functions.
Sinc functions
The family of functions (often called sinc functions) shown in Fig., 4 è
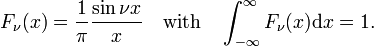
Questa famiglia converge alla funzione di delta per aumentare ν
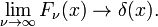
Questo limite porta facilmente alla integrali di Fourier e la rappresentazione della funzione di delta:
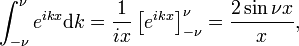
che
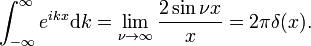
La funzione delta di Dirac è la trasformata di Fourier dell’unità di funzione f(x) = 1.
Derivate della funzione delta
Si consideri una funzione differenziabile f(x) che svanisce a più e meno infinito.,d=”ed7dae11d6″>
Nello stesso modo come dimostra il fatturato regola e Hermiticity di meccanica quantistica slancio operatore 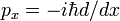 , che vi abbiamo mostrato qui che d/dx è anti-Hermitiane,
, che vi abbiamo mostrato qui che d/dx è anti-Hermitiane,
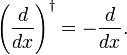
Infatti, quando scriviamo l’integrale come un prodotto interno, segue la parziale integrazione e la scomparsa di f(x) sull’integrazione limiti che
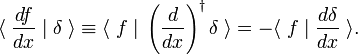
Questo fatturato regola è utilizzato come definizione di derivata della funzione delta,
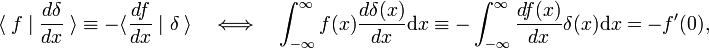
dove il primo indica la derivata prima di f(x)., Secondo la definizione della funzione delta la derivata prima viene valutata in x = 0. Utilizzando m volte il fatturato regola, ne consegue che l’mth derivata della funzione delta è definito da
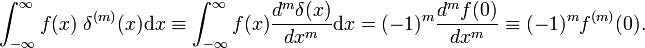
Proprietà della derivata
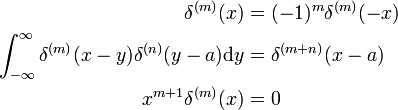
Questi risultati può essere dimostrato facendo la sostituzione x → −x e l’uso del fatturato regola d/dx (vedi sopra).,
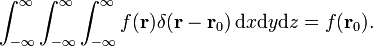
I tre-dimensionale funzione di delta può essere factorized
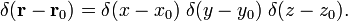
In coordinate polari sferiche
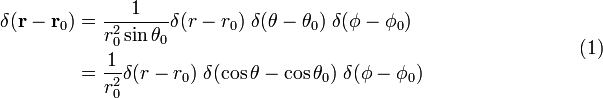
la Prova dell’equazione (1)
Scrivere
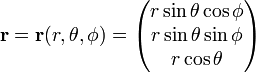
Il Jacobiano (Jacobi determinante) di questa trasformazione da coordinate Cartesiane a coordinate polari sferiche è
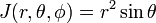
prendere in Considerazione
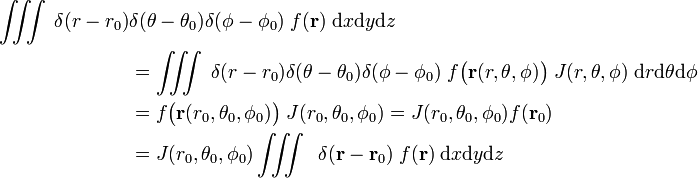
che
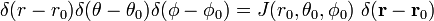
e
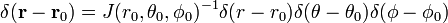
L’ultima riga equazione (1) segue dalla catena regola.,
I seguenti utile e spesso applicato proprietà è dimostrato qui,
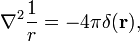
dove ∇2 è l’operatore di Laplace in tridimensionale di coordinate Cartesiane e r è la lunghezza del r.