Le funzioni logaritmiche sono gli inversi delle funzioni esponenziali. L’inverso della funzione esponenziale y = ax è x = ay. La funzione logaritmica y = logax è definita come equivalente all’equazione esponenziale x = ay. y = logax solo nelle seguenti condizioni: x = ay ,a> 0 e a a 1. Si chiama funzione logaritmica con base a.
Considera cosa significa l’inverso della funzione esponenziale: x = ay., Dato un numero x e una base a, a quale potenza y deve essere aumentata a x uguale? Questo esponente sconosciuto, y, è uguale a logax. Quindi vedi che un logaritmo non è altro che un esponente. Per definizione, alogax = x, per ogni x reale > 0.
Di seguito sono riportati i grafici del modulo y = logax quando a> 1 e quando 0< a< 1. Si noti che il dominio consiste solo dei numeri reali positivi e che la funzione aumenta sempre all’aumentare di x.,
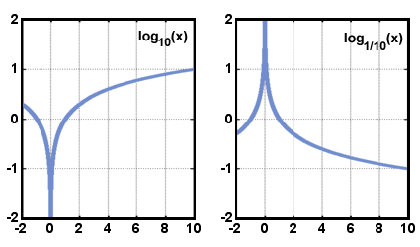
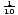 x.
x. Il dominio di una funzione logaritmica è numeri reali maggiori di zero e l’intervallo è numeri reali. Il grafico di y = logax è simmetrico al grafico di y = ax rispetto alla linea y = x. Questa relazione è vera per qualsiasi funzione e la sua inversa.,
Here are some useful properties of logarithms, which all follow from identities involving exponents and the definition of the logarithm. Remember a > 0, and x > 0.
logarithm
| loga1 = 0. |
| logaa = 1. |
| loga(ax) = x., |
| alogax = x. |
| loga(bc) = logab + logac. |
loga(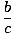 ) = logab – logac., ) = logab – logac., |
| loga(xd) = d logax |
Una naturale funzione logaritmica è una funzione logaritmica con base e. f (x) = logex = ln x, dove x > 0. ln x è solo una nuova forma di notazione per i logaritmi con base e. La maggior parte delle calcolatrici ha pulsanti etichettati “log” e “ln”. Il pulsante” log “presuppone che la base sia dieci, e il pulsante “ln”, ovviamente, lascia che la base sia uguale a e., La funzione logaritmica con base 10 è talvolta chiamata funzione logaritmica comune. È usato ampiamente perché il nostro sistema di numerazione ha base dieci. I logaritmi naturali sono visti più spesso nel calcolo.
Esistono due formule che consentono di modificare la base di una funzione logaritmica. Il primo afferma questo: logab = 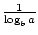 . La formula più famosa e utile per cambiare le basi è comunemente chiamata il cambiamento della formula di base. Consente di modificare la base di una funzione logaritmica in qualsiasi numero reale positivo 1 1. Si afferma che logax =
. La formula più famosa e utile per cambiare le basi è comunemente chiamata il cambiamento della formula di base. Consente di modificare la base di una funzione logaritmica in qualsiasi numero reale positivo 1 1. Si afferma che logax = 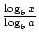 ., In questo caso, a, b e x sono tutti numeri reali positivi e a, b 1 1.
., In questo caso, a, b e x sono tutti numeri reali positivi e a, b 1 1.
Nella prossima sezione, discuteremo alcune applicazioni di funzioni esponenziali e logaritmiche.