Iniziamo con un esempio semplice, diciamo che vogliamo moltiplicare (2x-3)3. Questo non sarebbe troppo difficile da fare a mano lunga, ma usiamo il teorema binomiale in modo che quando incontri espansioni più grandi come i binomi sollevati ai poteri 4, 5, 6, … saprai esattamente cosa fare.
Per iniziare, devi identificare i due termini dal tuo binomio (le posizioni x e y della nostra formula sopra) e la potenza (n) a cui stai espandendo il binomio.,
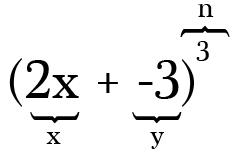
Ad esempio, per espandere (2x-3)3, i due termini sono 2x e -3 e la potenza, o il valore n, è 3. Nota che ogni volta che hai una sottrazione nel tuo binomio è così importante ricordare di includere il meno come simbolo negativo sul termine di accompagnamento.
La cosa meravigliosa del teorema binomiale è che ci permette di trovare il polinomio espanso senza moltiplicare un gruppo di binomi insieme. Abbastanza pulito, giusto?, Si scopre che il numero di termini nel tuo polinomio espanso sarà sempre uno in più della potenza che stai espandendo. Ciò significa che creeremo un polinomio con 4 termini poiché la potenza in questo esempio è 3.
Ogni termine avrà un (2x) e (-3) così come la formula “n scegli k” dove n=3. Puoi andare avanti e scriverlo 4 volte, uno per ogni termine, lasciando il valore k in “n scegli k” e le potenze vuote per il momento.
Successivamente ti consigliamo di compilare i valori k e le potenze. Qui puoi seguire la formula di sommatoria, aumentando la potenza per ogni termine., Ma è abbastanza facile da seguire solo i modelli.
I valori k in “n scegli k”, inizieranno con k=0 e aumenteranno di 1 in ogni termine. L’ultimo termine dovrebbe terminare con n uguale a k, in questo caso n=3 e k=3.
Quindi dobbiamo aggiungere i poteri su (2x) e (-3).
L’accensione (2x) inizierà con il valore n, quindi in questo caso 3, e diminuirà di 1 su ogni termine, fino ad arrivare a zero. L’accensione (-3) inizierà con zero e aumenterà di uno ogni volta fino ad arrivare a n, o 3 in questo problema.,

Poiché qualsiasi valore elevato alla potenza zero è uguale a 1, è possibile semplificare i termini con potenze pari a zero.

Avanti andare avanti e applicare i poteri e semplificare ove possibile.,

il Triangolo di Pascal di scelta rapida

L’ultima parte è quello di risolvere le combinazioni formula. Il modo ovvio per farlo è applicare la formula delle combinazioni per ogni problema. Ma stiamo andando a prendere una bella scorciatoia qui usando il Triangolo di Pascal.
Il Triangolo di Pascal è un triangolo semplice ma potente formato creando un triangolo con tre 1 per iniziare., Per ogni riga in seguito basta scrivere 1 su entrambe le estremità e trovare il numero centrale aggiungendo i due valori direttamente sopra di esso.

Ora ecco la parte buona. Nascosto all’interno del Triangolo di Pascal sono tutte le risposte a qualsiasi “n scegliere k”! E ‘ come un piccolo cheatsheet segreto!
Lo schema seguente mostra dove si trovano i “n choose k” nascosti.,

Per il nostro problema abbiamo bisogno di risolvere per: 3 scegliere 0, 3 scegliere 1, 3 scegliere 2, e 3 scegliere 3. Quali sono tutti i valori nella 4a riga. Quindi tutto quello che dobbiamo fare è guardare alla 4a riga del Triangolo di Pascal e abbinare le risposte.
La 4a riga ha i valori: 1, 3, 3, 1. Quindi sostituirò le risposte per il nostro n scegliere k.,

Infine, tutto ciò che devi fare è moltiplicare e semplificare ogni termine fino alla sua forma più semplice. Non dimenticate di controllare la risposta finale per assicurarsi che i poteri su ogni termine ancora aggiungere al grado del vostro binomio originale! Fidati di me, è incredibilmente facile commettere un errore di trascrizione in questo tipo di problema 😉
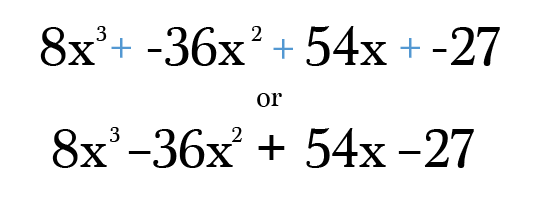
un altro esempio?,
Nel video qui sopra, ti mostro come usare il Teorema binomiale per espandere il binomio (x – 3y)⁵. Inoltre vi mostro alcuni trucchi aggiuntivi per rimanere organizzato e un paio di controlli rapidi è possibile utilizzare per identificare facilmente gli errori più comuni.
Grazie per la lettura!
❤ RIMANERE IN CONTATTO ❤
Rimani aggiornato con tutto ciò che Hacks matematica è fino a!