In queste pagine esaminiamo alcuni concetti interessanti, guardiamo lo spazio curvo: cosa significa lo spazio curvo, come possiamo dire se uno spazio è curvo dall’interno o dall’esterno.
Guardiamo come possiamo incorporare il tipo di spazio all’interno di un altro e vedere che possiamo mappare tra diversi spazi in modi diversi.
Guardiamo anche alla compattazione e a come possiamo rappresentare vettori infinitamente grandi e infinitesimalmente piccoli nei nostri spazi in modi che non non portano a singolarità e altri problemi.,
Questi concetti si rivelano utili, anche quando stiamo lavorando con lo spazio piatto, troveremo modi per rappresentare vettori e piani che non attraversano l’origine. Questo ci dà modi per rappresentare rotazioni e traduzioni come una singola operazione.
L’altra applicazione è lo spazio-tempo relativistico.
Geometria Rienmanniana
Nella geometria Rienmanniana lo spazio può curvare in luoghi diversi (vedi varietà) qui guardiamo le geometrie in cui la curva dello spazio è costante.,
Eulidean Geometria
spazio piatto
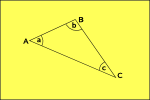
Geometria Iperbolica
spazio curve verso l’esterno
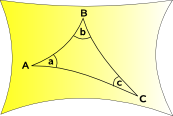
Geometria Sferica e la Geometria Ellittica
spazio curve verso l’interno
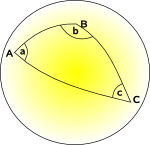
In una curva (Non Euclidea) geometria non riusciamo a trovare un set di coordinate tra loro perpendicolari, dove l’coordinare le linee sono tutte parallele tra loro e in cui ogni quadrato della griglia ha la stessa area., Potremmo forse trovare un sistema di coordinate in cui possiamo fare alcuni di questi, ma non tutti.
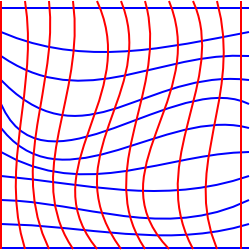
Questo diagramma cerca di illustrare questa situazione in 2 dimensioni, anche se è un po ‘ fuorviante, perché l’abbiamo disegnata su un piano in modo da poter disegnare coordinate rettangolari.
Per cercare di illustrare una situazione in cui questo è impossibile potremmo pensare a un piano bidimensionale che è stato allungato nella terza dimensione.,

In questa situazione possiamo scegliere le coordinate che formano una griglia rettangolare quando proiettate su un piano orizzontale, tuttavia, ad una persona che vive nella superficie, alcuni dei quadrati della griglia appariranno avere un’area più ampia di altri e le linee della griglia potrebbero non apparire parallele. Non esiste un sistema di coordinate bidimensionale che conservi linee parallele, angoli e aree allo stesso tempo.,
Un esempio simile sta cercando di mappare la superficie della terra, possiamo usare le linee di latitudine e longitudine ma le linee di longitudine si avvicinano più vicino ai poli.
In questi casi potremmo lavorare in termini di coordinate dimensionali 3 e questo è un approccio che prenderemo con alcuni tipi di geometrie non euclidee. È spesso possibile incorporare una particolare geometria in una geometria dimensionale superiore per renderla più euclidea.,
A volte accade che, quando guardiamo una geometria su larga scala, non sia euclidea, ma se la guardiamo su una scala sempre più piccola, allora si approssima a una geometria euclidea. Per fare ciò dobbiamo trovare un sistema di coordinate in cui gli angoli siano preservati in ogni punto, cioè le linee di coordinate orizzontali e verticali devono sempre intersecarsi a 90° anche se le linee potrebbero non essere diritte. Questo è noto come una geometria conforme. In questo tipo di geometria possiamo almeno definire un sistema di coordinate locali.,
In relazione a questo è se la geometria può essere differenziata e integrata, una condizione per questo è che deve essere ben comportata e non avere salti improvvisi ecc. Alcune geometrie e sistemi di coordinate possono essere ben comportati in alcuni punti, ma hanno singolarità ecc.
Per la discussione su come viene misurata la curvatura vedere questa pagina.
Notazione matematica
Come affrontiamo le geometrie in cui non possiamo usare tutte le regole che si applicano alla geometria euclidea?,
Un approccio è usare la notazione tensoriale, questo fornisce convenzioni e notazioni che ci aiutano a passare da diversi sistemi di coordinate. Un sistema di coordinate ortogonali, locale a qualsiasi punto, può essere definito utilizzando vettori di base che sono tangenti alle linee di coordinate.,Collettore
consultare questa pagina
la Relazione tra Iperbolico e Minkowski Geometrie
| Minkowski Geometria | Geometria Iperbolica | |
| punto | evento nello spazio di tempo | particella in moto uniforme |
| distanza tra due punti | spazio-intervallo di tempo tra due eventi | velocità relativa tra due particelle |
Terminologia
Qui guardiamo la terminologia come geometrie, gli spazi, i modelli, le proiezioni e la trasforma., È abbastanza difficile quando iniziamo a trattare con geometrie non euclidee perché usiamo una terminologia simile a quella a cui siamo abituati nello spazio euclideo convenzionale, ma i termini possono avere proprietà leggermente diverse.,prova
Elliptic Geometry
Modelli
Esempi:
- metà Superiore-modello di aereo
- modello del disco di Poincaré
- modello Proiettivo
- rivestimento Protettivo modello
Proiezioni
Proiezione Stereografica
Trasforma
Invariante
Esempi:
- Ciclo di Trasformazione
- Trasformazione di Lorentz
Parallelo Postulato
Se togliamo il parallelo postulato da Spazio Euclideo.,
Questo porta a:
- il postulato parallelo è falso
- gli angoli di un triangolo non si aggiungono a π
- per una forma di una data dimensione, in generale, non esiste una forma simile di una dimensione maggiore.,ttivo
conformazionale (disco di Poincaré ) le linee rette – geodesics segmenti di cerchio angolo conservazione angoli interni di un triangolo π-(α+β+γ)=CΔ la distanza tra due punti con