Gli automi finiti possono avere uscite corrispondenti ad ogni transizione. Ci sono due tipi di macchine a stati finiti che generano output −
- Macchina farinosa
- Macchina Moore
Macchina farinosa
Una macchina farinosa è un FSM il cui output dipende dallo stato attuale e dall’input presente.,
Può essere descritto da una tupla 6 (Q, ∑, O, δ, X, q0) dove −
-
Q è un insieme finito di stati.
-
∑ è un insieme finito di simboli chiamato alfabeto di input.
-
O è un insieme finito di simboli chiamato alfabeto di output.
-
δ è la funzione di transizione in ingresso dove δ: Q × → → Q
-
X è la funzione di transizione in uscita dove X: Q × → → O
-
q0 è lo stato iniziale da cui viene elaborato qualsiasi input (q0 Q Q).,b424468″>
Output
The state diagram of the above Mealy Machine is −
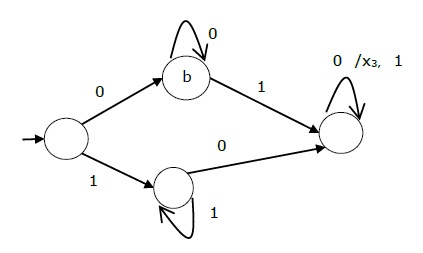
Moore Machine
Moore machine is an FSM whose outputs depend on only the present state.,
Una macchina di Moore può essere descritta da una tupla 6 (Q, ∑, O, δ, X, q0) dove −
-
Q è un insieme finito di stati.
-
∑ è un insieme finito di simboli chiamato alfabeto di input.
-
O è un insieme finito di simboli chiamato alfabeto di output.
-
δ è la funzione di transizione in ingresso dove δ: Q × → → Q
-
X è la funzione di transizione in uscita dove X: Q → O
-
q0 è lo stato iniziale da cui viene elaborato qualsiasi input (q0 Q Q).,iv>
Present state Next State Output Input = 0 Input = 1 → a b c x2 b b d x1 c c d x2 d d d x3 The state diagram of the above Moore Machine is −
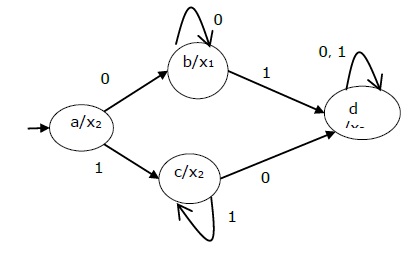
Mealy Machine vs., Macchina Moore
La seguente tabella evidenzia i punti che differenziano una macchina farinosa da una macchina Moore.
Macchina farinosa Macchina Moore L’uscita dipende sia dallo stato attuale che dall’ingresso attuale L’uscita dipende solo dallo stato attuale. Generalmente, ha meno stati rispetto alla macchina di Moore. Generalmente, ha più stati rispetto alla macchina farinosa., Il valore della funzione di output è una funzione delle transizioni e delle modifiche, quando viene eseguita la logica di input sullo stato attuale. Il valore della funzione di output è una funzione dello stato corrente e delle modifiche ai bordi dell’orologio, ogni volta che si verificano cambiamenti di stato. Le macchine farinose reagiscono più velocemente agli input. Generalmente reagiscono nello stesso ciclo di clock. Nelle macchine Moore, è necessaria più logica per decodificare le uscite con conseguente più ritardi del circuito. Generalmente reagiscono un ciclo di clock più tardi., Moore Machine to Mealy Machine
Algoritmo 4
Input − Moore Machine
Output − Mealy Machine
Step 1 − Prendi un formato di tabella di transizione della macchina Mealy vuota.
Fase 2-Copiare tutti gli stati di transizione macchina Moore in questo formato di tabella.
Fase 3-Controllare gli stati presenti e le loro uscite corrispondenti nella tabella di stato macchina Moore; se per uno stato Qi uscita è m, copiarlo nelle colonne di uscita della tabella di stato macchina farinosa ovunque Qi appare nello stato successivo.,der the following Moore machine −
Present State Next State Output a = 0 a = 1 → a d b 1 b a d 0 c c c 0 d b a 1 Now we apply Algorithm 4 to convert it to Mealy Machine.,8″>
Output
Mealy Machine to Moore Machine
Algorithm 5
Input − Mealy Machine
Output − Moore Machine
Step 1 − Calculate the number of different outputs for each state (Qi) that are available in the state table of the Mealy machine.,
Passo 2-Se tutte le uscite di Qi sono uguali, copia stato Qi. Se ha n uscite distinte, rompere Qi in n stati come Qin dove n = 0, 1, 2…….
Passo 3-Se l’uscita dello stato iniziale è 1, inserire un nuovo stato iniziale all’inizio che dà 0 uscita.,b424468″>
Output
Here, states ‘a’ and ‘d’ give only 1 and 0 outputs respectively, so we retain states ‘a’ and ‘d’., Ma gli stati ” b ” e ” c ” producono output diversi (1 e 0). Quindi, dividiamo b in b0, b1 e c in c0, c1.,”>
Output