
Ti sei mai chiesto come può nevicare a temperature sopra lo zero? Bene, la spiegazione ingenua è che ci vuole semplicemente tempo perché i fiocchi di neve si sciolgano una volta che penetrano al di sopra dell’aria gelida, mentre scendono verso il basso fino a terra. Questo, naturalmente, è il motivo per cui la grandine può cadere nella stagione calda. Semplicemente, le pietre di grandine cadono velocemente, troppo velocemente per lasciare che l’aria calda sciolga la grandine. Questa non è la spiegazione principale, tuttavia, per il motivo per cui può nevicare quando è sopra lo zero.,
Dalla figura sottostante, è evidente che c’è una chiara dipendenza dall’umidità: più è secca, più calda può essere mentre nevica. Ciò implica che il fattore principale, almeno in condizioni asciutte, ha a che fare con l’umidità. E questo fattore è l’evaporazione. Più specificamente, mentre i fiocchi di neve scendono, evaporano. Questo processo prende calore e mantiene i fiocchi freddi.
Quindi, se vogliamo calcolare la temperatura massima, dobbiamo stimare il bilancio termico netto del fiocco. Innanzitutto, mentre i fiocchi viaggiano in un ambiente caldo, guadagnano calore dall’ambiente circostante attraverso la conduzione., In secondo luogo, il calore viene utilizzato per far evaporare i fiocchi, raffreddandoli in tal modo. Se il “dissipatore” di calore di evaporazione è più grande della conduzione del calore, i fiocchi rimarranno congelati.
Si scopre che questo può essere facilmente calcolato. No, non è semplice calcolare la conduzione del calore o il calore di evaporazione, ma il rapporto è, poiché vari fattori geometrici sconosciuti si annullano.
Se non ti interessa il calcolo (perché non sei un maniaco della scienza), puoi semplicemente visitare la pagina della calcolatrice.
Se ti interessa, ecco la derivazione., Supponiamo che il flusso attorno ai fiocchi sia tale che uno strato limite di larghezza d si formi attorno ad esso. Il flusso di calore $F_H$ a fiocco (ad esempio, J/sec in MKS) sarà dato dalla legge di Fourier:
dove $\kappa$ è il calore coefficiente di diffusione dell’aria (ad esempio, m2/sec in MKS), c è la capacità termica dell’aria (J/kg in MKS), A è l’area della superficie dello strato limite in tutto il flake, mentre ∆ T è la differenza di temperatura tra il fiocco e l’ambiente.,
Allo stesso modo, si può usare la legge di Fick per ottenere la diffusione del vapore acqueo dal fiocco (dove la temperatura è vicina al congelamento e l’umidità relativa è del 100%), all’ambiente circostante, dove la temperatura è più alta e l’umidità relativa più bassa:
Qui, D è il coefficiente di diffusione dell’acqua (ad esempio, m2/sec in MKS) e ρ è la densità del vapore acqueo (kg/m3 in MKS).,
Il ghiaccio evaporante richiede calore, quindi, se c’è un flusso di massa di vapore acqueo di Φ dal fiocco, richiederebbe calore ad una velocità di F F_w = \epsilon \Phi where dove $\epsilon is è il calore di vaporizzazione del ghiaccio (J/kg in MKS).
La temperatura più alta al di sopra della quale il fiocco di neve si scioglie, è la temperatura per la quale i due flussi di calore sono uguali:
Si noti che la geometria del flusso attorno al fiocco si annulla, poiché entrambi i flussi di calore dipendono da d e A allo stesso modo., Questo sarebbe il caso anche se lo strato limite attorno al fiocco è complesso in modo tale che d dipenda effettivamente dalla direzione. Quindi,
dove \ \ rho_{sat} is è la densità del vapore acqueo di saturazione.
Collegando i numeri (che si possono trovare ad esempio nel manuale CRC di chimica e fisica), si ottiene un’equazione implicita per la temperaturaperché la densità del vapore acqueo di saturazione dipende anche dalla temperatura., Possiamo semplificare le cose se invece chiediamo qual è l’umidità relativa necessaria per mantenere il fiocco congelato ad una data temperatura. È:
dove T T_C is è la temperatura in gradi Celsius.
Questa funzione può essere vista nella figura seguente, insieme ai dati di Matsuo e Sasyo, 1981. Come si può vedere dalla figura, il grafico calcolato è approssimativamente il limite inferiore al di sotto del quale non c’è pioggia di sorta. A temperature più calde, c’è un mix., Fino a circa 1°C sopra la linea di non fusione, c’è per lo più neve mentre tra circa 1°C e 2°C sopra la linea, è per lo più pioggia, ma la neve è possibile. Questi eventi potrebbero essere dovuti a effetti aggiuntivi, come forti downdraft, tempo necessario per sciogliere la neve, ecc.
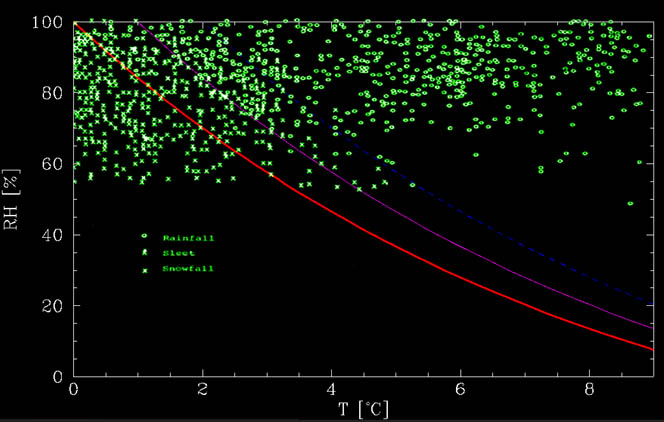
Quindi, se vogliamo osservare la neve calda, sono necessarie condizioni molto asciutte. Ad esempio, se l’umidità del terreno è solo circa il 20% (molto raro, perché se ci sono precipitazioni, l’atmosfera è generalmente bagnata!) quindi potrebbe nevicare a 8 ° C (o 46°F per gli utenti inglesi).,
Un altro requisito è che da nessuna parte lungo la discesa l’aria supera la linea di no melt. Se lo fa, il fiocco si scioglierà naturalmente.
Se la temperatura sale sopra lo zero, non ci sono parametri con cui il tipo di precipitazione può essere determinato per certezza. Tutto ciò che possiamo quindi prevedere è la probabilità che la neve cada effettivamente. Questo può essere fatto utilizzando i risultati di Häggmark e Ivarsson (1997), corretti solo per utilizzare il bulbo congelato e non la temperatura del bulbo umido.
La linea di fondo è una calcolatrice con cui si può stimare la probabilità di neve.,