Trova tutte le radici di una funzione polinomiale
Usavpasolve per trovare tutte le soluzioni alla funzione f(x)=6×7-2×6+3×3-8.
syms f(x)f(x) = 6*x^7-2*x^6+3*x^3-8;sol = vpasolve(f)
vpasolve restituisce sette radici della funzione, come previsto, perché la funzione è un polinomio di grado sette.,
Trova zeri di una funzione Nonpolynomial Usando intervalli di ricerca e punti di partenza
Un grafico della funzione f(x)=e(x / 7)cos(2x) rivela zeri periodici, con pendenze crescenti ai punti zero all’aumentare di x.
syms xh = fplot(exp(x/7)*cos(2*x),);grid on
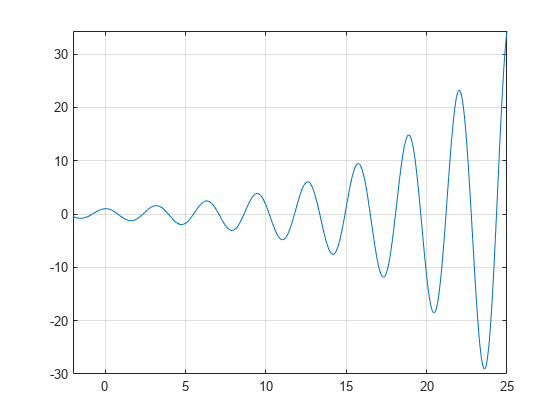
Uso vpasolve per trovare uno zero della funzione f. Si noti chevpasolve restituisce solo una soluzione di un’equazione non lineare, anche se esistono più soluzioni., On repeated calls, vpasolve returns the same result.
f = exp(x/7)*cos(2*x);for k = 1:3 vpasolve(f,x)end
ans = -7.0685834705770347865409476123789-vpa('7.0685834705770347865409476123789')
ans = -7.0685834705770347865409476123789-vpa('7.0685834705770347865409476123789')
ans = -7.0685834705770347865409476123789-vpa('7.0685834705770347865409476123789')
To find multiple solutions, set the option 'Random' to true. This makes vpasolve choose starting points randomly., For information on the algorithm that chooses random starting points, see Algorithms on the vpasolve page.
for k = 1:3 vpasolve(f,x,'Random',true)end
ans = -226.98006922186256147892598444194-vpa('226.98006922186256147892598444194')
ans = 98.174770424681038701957605727484vpa('98.174770424681038701957605727484')
ans = 52.621676947629036744249276669932vpa('52.621676947629036744249276669932')
To find a zero close to x=10, set the starting point to 10.,
vpasolve(f,x,10)
ans = 10.210176124166828025003590995658vpa('10.210176124166828025003590995658')
Per trovare lo zero vicino a x=1000, impostare il punto di partenza per 1000.
vpasolve(f,x,1000)
ans = 999.8118620049516981407362567287vpa('999.8118620049516981407362567287')
Per trovare lo zero nell’intervallo 15≤x≤25, impostare l’intervallo di ricerca .,
vpasolve(f,x,)
ans = 21.205750411731104359622842837137vpa('21.205750411731104359622842837137')
Per trovare più zeri nell’intervallo non è possibile chiamare vpasolve ripetutamente perché restituisce lo stesso risultato su ogni chiamata, come illustrato in precedenza. Impostare invece l’intervallo di ricerca e impostare 'Random'sutrue.,
for k = 1:3 vpasolve(f,x,,'Random',true)end
ans = 21.205750411731104359622842837137vpa('21.205750411731104359622842837137')
ans = 21.205750411731104359622842837137vpa('21.205750411731104359622842837137')
ans = 16.493361431346414501928877762217vpa('16.493361431346414501928877762217')
Perché 'Random' seleziona i punti di partenza in modo casuale, la stessa soluzione potrebbe essere trovato su chiamate successive.,
Trova tutti gli zeri in un intervallo di ricerca specificato
Crea una funzionefindzeros per trovare sistematicamente tutti gli zeri perf in un determinato intervallo di ricerca, entro una tolleranza di errore specificata. La funzione inizia con l’intervallo di ricerca di input e chiama vpasolve per trovare uno zero. Quindi, divide l’intervallo di ricerca in due attorno al valore zero e si chiama ricorsivamente con i nuovi intervalli di ricerca come input per trovare più zeri.
La funzione è spiegata sezione per sezione qui.,
Dichiarare la funzione con i tre ingressi e una uscita. Il primo ingresso è la funzione, il secondo ingresso è l’intervallo e il terzo ingresso opzionale consente di specificare l’errore tra uno zero e i limiti superiore e inferiore generati da esso.
function sol = findzeros(f,range,err)
Se non si specifica l’argomento opzionale per la tolleranza agli errori,findzerosimpostaerra0.001.
if nargin < 2 err = 1e-3;end
Trova uno zero nell’intervallo di ricerca usando vpasolve.,
sol = vpasolve(f,range);
Sevpasolve non trova uno zero, uscire.
if(isempty(sol)) return
Sevpasolve trova uno zero, dividere l’intervallo di ricerca in due intervalli di ricerca sopra e sotto lo zero.
else lowLimit = sol-err; highLimit = sol+err;
Chiama findzeros con l’intervallo di ricerca inferiore. Sefindzeros restituisce zeri, copiare i valori nell’array della soluzione e ordinarli.
temp = findzeros(f,,1); if ~isempty(temp) sol = sort(); end
Chiama findzeros con l’intervallo di ricerca più alto., Sefindzeros restituisce zeri, copiare i valori nell’array della soluzione e ordinarli.
temp = findzeros(f,,1); if ~isempty(temp) sol = sort(); end returnendend
L’intera funzionefindzeros è la seguente. Salvare questa funzione comefindzeros.m nella cartella corrente.
Ottenere soluzioni con precisione arbitraria
Utilizzare digits per impostare la precisione delle soluzioni restituite da vpasolve., Per impostazione predefinita,vpasolve restituisce le soluzioni con una precisione di 32 cifre significative.
f = exp(x/7)*cos(2*x);vpasolve(f)
ans = -7.0685834705770347865409476123789-vpa('7.0685834705770347865409476123789')
Uso digits per aumentare la precisione a 64 cifre significative. Quando si modifica digits, assicurarsi di salvare il valore corrente in modo da poterlo ripristinare.,
Quindi, modificare la precisione delle soluzioni a 16 cifre significative.
digits(16)
Risolvi equazioni multivariate usando gli intervalli di ricerca
Considera il seguente sistema di equazioni.
z=10(cos(x)+cos(y))z=x+y2-0.1x2yx+y-2.7=0
Un grafico delle equazioni per 0≤x≤2.5 e 0≤x≤2.5 mostra che le tre superfici si intersecano in due punti., Per visualizzare meglio la trama, utilizzareview. Per ridimensionare i valori della mappa colori, utilizzarecaxis.
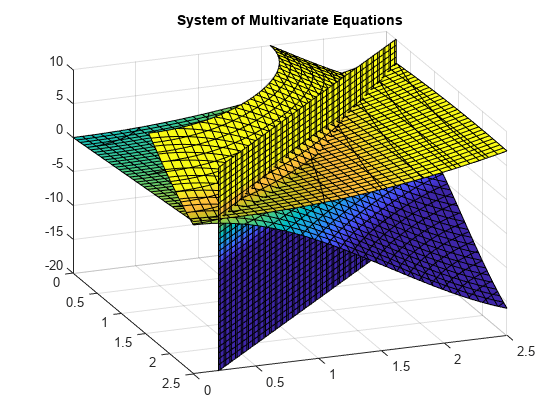
Utilizzare vpasolve per trovare un punto in cui le superfici si intersecano. La funzione vpasolve restituisce una struttura. Per accedere al x -, y -, e z -valori della soluzione, indice nella struttura.,
sol = vpasolve(equations);
Per cercare una regione dello spazio della soluzione, specificare gli intervalli di ricerca per le variabili. Se si specificano gli intervalli 0≤x≤1.5 e 1.5≤y≤2.5, la funzionevpasolve cerca l’area delimitata mostrata.

Utilizzare vpasolve per trovare una soluzione per questo intervallo di ricerca. Per omettere un intervallo di ricerca per z, impostare il terzo intervallo di ricerca su .,
Per trovare più soluzioni, impostare l’opzione'Random' su true. Ciò rendevpasolve utilizzare punti di partenza casuali su esecuzioni successive. L’opzione'Random' può essere utilizzata in combinazione con gli intervalli di ricerca per renderevpasolve utilizzare punti di partenza casuali all’interno di un intervallo di ricerca. Poiché'Random' seleziona i punti di partenza in modo casuale, la stessa soluzione potrebbe essere trovata nelle chiamate successive., Chiama ripetutamentevpasolve per assicurarti di trovare entrambe le soluzioni.
Tracciare le equazioni. Sovrapponi le soluzioni come un grafico a dispersione di punti con marcatori gialli X usando scatter3. Per visualizzare meglio la trama, rendere trasparenti due delle superfici usandoalpha. Ridimensiona la mappa dei colori ai valori della trama usandocaxis e cambia la prospettiva usandoview.
vpasolve trova soluzioni all’intersezione delle superfici formate dalle equazioni come mostrato.,

Lastly, restore the old value of digits for further calculations.
digits(digitsOld)