Sezioni trasversali

Proprietà delle aree

Centroide

Il centroide di una forma rappresenta il punto su cui l’area della sezione è uniformemente distribuita. Se l’area è doppiamente simmetrica su due assi ortogonali, il centroide si trova all’intersezione di quegli assi. Se l’area è simmetrica su un solo asse, il centroide si trova da qualche parte lungo quell’asse (l’altra coordinata dovrà essere calcolata)., Se l’esatta posizione del baricentro non può essere determinato, mediante ispezione, può essere calcolato:

dA dove rappresenta l’area di un infinitesimamente piccolo elemento, A è l’area totale della sezione trasversale, e x e y sono le coordinate dell’elemento dA rispetto all’asse di interesse.,

Le posizioni centroidali delle sezioni trasversali comuni sono ben documentate, quindi in genere non è necessario calcolare la posizione con le equazioni di cui sopra., di forme di base di cui centroidal luoghi sono noti rispetto a qualche punto di riferimento, quindi il centroidal posizione del composito sezione trasversale può essere calcolato come:

dove xc,io e yc,io sono coordinate rettangolari di centroidal posizione della i-esima sezione rispetto al punto di riferimento, e Ai è l’area della i-esima sezione.,

Distanza centroidale

La distanza centroidale, c, è la distanza dal centroide di una sezione trasversale alla fibra estrema., Il centroidal distanza in direzione y per una sezione rettangolare è mostrato nella figura di seguito:

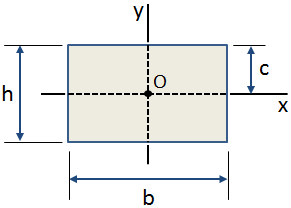
usi Comuni per centroidal distanza includono:

• calcolare la massima sollecitazione di flessione in una sezione trasversale
• calcolo del valore del primo momento di area, Q, al di sopra di un punto a croce sezione per determinare la sollecitazione di taglio, a quel punto

Primo Momento di Area

Il primo momento di un territorio rispetto a un asse di interesse è calcolato come:

Qx = ∫ y dA

Qy = ∫ x dA

dove Qx è il primo momento intorno all’asse x e Qy è il primo momento intorno all’asse y.,Se l’area è costituita da un insieme di forme di base di cui centroidal luoghi sono noti rispetto all’asse di interesse, quindi il primo momento del composito area può essere calcolata come:

Nota che il primo momento l’area è utilizzata per il calcolo del baricentro di una sezione trasversale rispetto ad alcuni di origine (come discusso in precedenza)., Il primo momento viene utilizzato anche quando si calcola il valore della sollecitazione di taglio in un particolare punto della sezione trasversale. In questo caso, il primo momento viene calcolato per un’area che costituisce una porzione più piccola della sezione trasversale, dove l’area è delimitata dal punto di interesse e dalla fibra estrema (superiore o inferiore) della sezione trasversale. Il primo momento è calcolato su un asse che passa attraverso il centroide della sezione trasversale.,

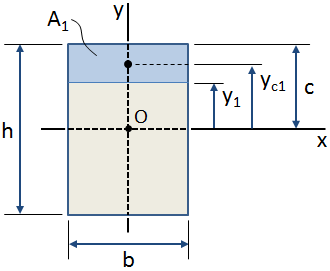
Nella figura sopra, l’area blu ombreggiata è l’area di interesse all’interno della sezione trasversale complessiva.,nt di questa area rispetto all’asse x (che passa attraverso la sezione trasversale del baricentro, il punto O, nella figura di sopra) è calcolata come:

Se il centroidal ubicazione dell’area di interesse è noto, quindi il primo momento di area rispetto all’asse può essere calcolato come (fare riferimento alla figura riportata sopra):

va notato che il primo momento di un’area sarà positivo o negativo, a seconda della posizione della posizione dell’area rispetto all’asse di interesse., Pertanto, il primo momento dell’intera area di una sezione trasversale rispetto al proprio centroide sarà zero.

Area Momento di inerzia

Il secondo momento di area, più comunemente noto come momento di inerzia, I, di una sezione trasversale è un’indicazione della capacità di un membro strutturale di resistere alla flessione.,(Nota 1) Ix e Iy sono i momenti di inerzia su x e y, rispettivamente, ed è calcolato:

Ix = ∫ y2 dA

Iy = ∫ x2 dA

dove x e y sono le coordinate dell’elemento dA rispetto all’asse di interesse.

Più comunemente, i momenti di inerzia sono calcolati rispetto al centroide della sezione. In questo caso sono indicati come momenti di inerzia centroidali e sono indicati come Icx per l’inerzia sull’asse x e Icy per l’inerzia sull’asse Y.,

I momenti di inerzia delle sezioni trasversali comuni sono ben documentati, quindi in genere non è necessario calcolarli con le equazioni di cui sopra. Le proprietà di diverse sezioni trasversali comuni sono riportate alla fine di questa pagina.

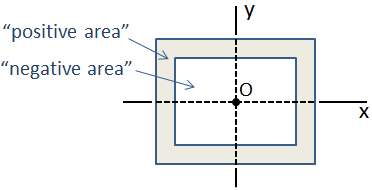
Se una sezione trasversale è composta da un insieme di forme di base i cui centroidi sono tutti coincidenti, allora il momento di inerzia della sezione composita è semplicemente la somma dei singoli momenti di inerzia. Un esempio di questo è una trave a scatola che consiste di due sezioni rettangolari, come mostrato di seguito., In questo caso, la sezione esterna ha “area positiva” e la sezione interna ha “area negativa”, quindi il momento di inerzia composito è la sottrazione del momento di inerzia della sezione interna dalla sezione esterna.

Nel caso di una sezione composita più complicata in cui le posizioni centroidali non sono coincidenti, il momento di inerzia può essere calcolato utilizzando il teorema dell’asse parallelo.

È importante non confondere il momento di inerzia di un’area con il momento di inerzia di massa di un corpo solido., Il momento di inerzia dell’area indica la resistenza di una sezione trasversale alla flessione, mentre il momento di inerzia della massa indica la resistenza di un corpo alla rotazione.,

Asse Parallelo Teorema

Se il momento di inerzia della sezione trasversale su un asse centrale è noto, l’asse parallelo teorema può essere utilizzato per calcolare il momento di inerzia su qualsiasi asse parallelo:

dove Ic è il momento di inerzia attorno all’asse centrale, d è la distanza tra l’asse centrale e l’asse parallelo, e A è l’area della sezione trasversale.,

Se una sezione trasversale è composta da un insieme di forme di base i cui momenti centroidali di inerzia sono noti insieme alle distanze dei centroidi rispetto a un punto di riferimento, allora il teorema dell’asse parallelo può essere utilizzato per calcolare il momento di inerzia della sezione trasversale composita.

Ad esempio, un I-Beam può essere approssimato da 3 rettangoli, come mostrato di seguito. Poiché questa sezione composita è simmetrica su entrambi gli assi x e y, il centroide della sezione può essere posizionato mediante ispezione all’intersezione di tali assi. Il centroide si trova all’origine, O, nella figura.,

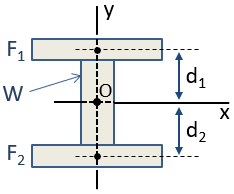
Il momento di inerzia della sezione composita può essere calcolato utilizzando il teorema dell’asse parallelo. Il momento d’inerzia centroidale della sezione attorno all’asse x, Icx, è calcolato come:

dove Icx termini sono i momenti di inerzia delle singole sezioni sulle loro centroidi l’orientamento dell’asse x, d termini sono le distanze dei singoli sezione centroidi per la sezione composta baricentro, e i termini sono le aree delle singole sezioni. Poiché il centroide della sezione W e il centroide della sezione composita sono coincidenti, d è zero per quella sezione e quindi non esiste un termine Ad2.,

È importante notare l’implicazione del teorema dell’asse parallelo che quando una singola sezione si sposta più lontano dal centroide della sezione composita, il contributo di quella sezione al momento di inerzia della sezione composita aumenta di un fattore d2. Pertanto, se l’intento è quello di aumentare il momento di inerzia di una sezione su un particolare asse, è più efficiente localizzare l’area il più lontano possibile da quell’asse. Questo spiega la forma di un I-Beam., Le flange sono i principali contributori al momento di inerzia e il nastro serve a separare le flange dall’asse di piegatura. Il web ha bisogno di mantenere un certo spessore tuttavia per evitare instabilità e perché il web prende una parte significativa dello stress di taglio nella sezione.

Momento polare di inerzia

Il momento polare di inerzia, I, di una sezione trasversale è un’indicazione della capacità di un membro strutturale di resistere alla torsione su un asse perpendicolare alla sezione., Il momento di inerzia polare per una sezione rispetto a un asse può essere calcolata nel modo seguente:

dove x e y sono le coordinate dell’elemento dA rispetto all’asse di interesse, e r è la distanza tra l’elemento dA e l’asse di interesse.,

anche se il momento di inerzia polare può essere calcolata utilizzando l’equazione di cui sopra, è in genere più conveniente per il calcolo si utilizza l’asse perpendicolare teorema che afferma che il momento di inerzia polare di un’area è la somma dei momenti di inerzia su due assi ortogonali che passa attraverso l’asse di interesse:

la Maggior parte dei casi, l’asse di interesse passa per il baricentro della sezione.,

Modulo di sezione

La massima sollecitazione di flessione in un fascio è calcolata come σb = Mc / Ic, dove c è la distanza dall’asse neutro alla fibra estrema, Ic è il momento di inerzia centroide e M è il momento flettente. Il modulo di sezione combina i termini c e Ic nell’equazione dello sforzo di flessione:

Usando il modulo di sezione, lo sforzo di flessione è calcolato come σb = M / S. L’utilità del modulo di sezione è che caratterizza la resistenza alla flessione di una sezione trasversale in un singolo termine., Ciò consente l’ottimizzazione della sezione trasversale di una trave per resistere alla flessione massimizzando un singolo parametro.

Raggio di rotazione

Il raggio di rotazione rappresenta la distanza dal centroide di una sezione alla quale tutta l’area potrebbe essere concentrata senza avere alcun effetto sul momento di inerzia.,>

A polar radius of gyration can also be calculated for problems involving torsion about a centroidal axis:

The rectangular radii of gyration can also be used to calculate the polar radius of gyration:

Proprietà di Comune di Sezioni Trasversali

La tabella di seguito fornisce le proprietà di comune di sezioni trasversali. Tabelle più estese possono essere trovate nei riferimenti elencati.

Le proprietà calcolate nella tabella includono area, momento di inerzia centroide, modulo di sezione e raggio di rotazione.,