laten we beginnen met een rechttoe rechtaan voorbeeld, stel dat we willen vermenigvuldigen (2x-3)3. Dit zou niet al te moeilijk zijn om long hand te doen, maar laten we de binomiale stelling gebruiken zodat wanneer je grotere expansies tegenkomt zoals binomials die zijn verhoogd tot de 4, 5, 6, … machten, je precies weet wat je moet doen.
om te beginnen, moet u de twee termen identificeren van uw binomiale (de x-en y-posities van onze formule hierboven) en de macht (n) waarnaar u de binomiale uitbreidt.,
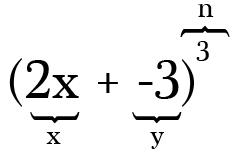
om bijvoorbeeld (2x-3)3 uit te breiden, zijn de twee termen 2x en -3 en is de macht, of de waarde n, 3. Merk op dat wanneer je een aftrekking in je binomiale is het oh zo belangrijk om te onthouden om de minus als een negatief symbool op de bijbehorende term.
het mooie aan de binomiale stelling is dat het ons in staat stelt de geëxpandeerde veelterm te vinden zonder een aantal binomials samen te vermenigvuldigen. Gaaf, hè?, Het blijkt dat het aantal termen in je geëxpandeerde veelterm altijd één meer zal zijn dan de macht die je uitdijt. Dat betekent dat we een veelterm maken met 4 termen aangezien de macht in dit voorbeeld 3 is.
elke term heeft een (2x) en (-3) en de formule “N choose k” waarbij n=3. Je kunt dat 4 keer opschrijven, één voor elke term, waarbij de K-waarde in “n kies k” blijft en de bevoegdheden op dit moment leeg zijn.
vervolgens wilt u de K-waarden en bevoegdheden invullen. Hier kunt u de sommatieformule volgen, waardoor de kracht voor elke term wordt verhoogd., Maar het is vrij gemakkelijk om gewoon de patronen te volgen.
De K-waarden in “n choose k” beginnen met k=0 en stijgen met 1 in elke term. De laatste term moet eindigen met n gelijk aan k, in dit geval n = 3 en k = 3.
vervolgens moeten we de bevoegdheden toevoegen aan (2x) en (-3).
de power on (2x) zal beginnen met de n-waarde, dus in dit geval 3, en zal afnemen met 1 op elke term, tot je op nul komt. De power on (-3) zal beginnen met nul en elke keer met een toenemen tot je bij n, of 3 in dit probleem.,

omdat elke waarde verhoogd tot de macht nul gelijk is aan 1, kunt u de termen vereenvoudigen met bevoegdheden van nul.

volgende ga je gang en pas de bevoegdheden toe en vereenvoudig waar mogelijk.,

The Pascal ‘ s Triangle Shortcut

het laatste deel is om de combinatieformule op te lossen. De voor de hand liggende manier om dit te doen is om de combinaties formule toe te passen voor elk probleem. Maar we gaan een kleine kortere weg nemen met de driehoek van Pascal.
Pascal ’s driehoek is een eenvoudige, maar krachtige driehoek gevormd door het creëren van een driehoek met drie 1′ s om te beginnen., Voor elke rij daarna schrijf je gewoon 1 ‘ s aan beide uiteinden, en vind je het middelste nummer (s) door de twee waarden direct erboven toe te voegen.

Hier is het goede deel. Verborgen in Pascal ’s driehoek zijn alle antwoorden op elke “n choose k”! Het is net een geheim cheatsheet!
het diagram hieronder laat zien waar de verborgen “n choose k’ s ” zich bevinden.,

voor ons probleem dat we moeten oplossen: 3 Kies 0, 3 Kies 1, 3 Kies 2, en 3 Kies 3. Dat zijn alle waarden in de 4e rij. We hoeven alleen maar naar de vierde rij van Pascals driehoek te kijken en de antwoorden te vergelijken.
de 4e rij heeft de waarden: 1, 3, 3, 1. Dus ik Vervang de antwoorden door onze n Kies k ‘ s.,

tot slot moet u elke term vermenigvuldigen en vereenvoudigen tot de eenvoudigste vorm. Vergeet niet om uw definitieve antwoord te controleren om ervoor te zorgen dat de bevoegdheden op elke term nog steeds toe te voegen aan de mate van uw oorspronkelijke binomiale! Geloof me, het is ongelooflijk eenvoudig om een transcriptiefout te maken in dit soort problemen;)
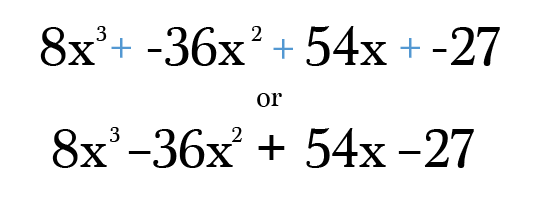
Need another example?,
in de video hierboven laat ik u zien hoe u de binomiale stelling gebruikt om de binomiale (x – 3y) ⁵ uit te breiden. Plus Ik toon u een aantal extra trucs om georganiseerd te blijven en een paar snelle controles die u kunt gebruiken om gemakkelijk gemeenschappelijke fouten te identificeren.
Bedankt voor het lezen!
❤ blijf verbonden ❤
blijf up-to-date met alles wat Math Hacks kan!