The Dirac deltafunctie is een functie die in 1930 werd geïntroduceerd door P. A. M. Dirac in zijn baanbrekende boek over kwantummechanica. Een fysisch model dat een deltafunctie visualiseert is een massaverdeling van de eindige totale massa M—de integraal over de massaverdeling., Wanneer de verdeling kleiner en kleiner wordt, terwijl M constant is, krimpt de massaverdeling tot een puntmassa, die per definitie nulomvang heeft en toch een eindige-gewaardeerde integraal heeft die gelijk is aan de totale massa M. In de grens van een puntmassa wordt de verdeling een Dirac-deltafunctie.
heuristisch gezien kan de Dirac-deltafunctie worden gezien als een uitbreiding van de Kronecker-delta van integrale indices (elementen van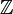 
) naar reële indices (elementen van 
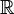)., Merk op dat de Kronecker−delta werkt als een “filter” in een sommatie:
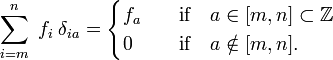
naar analogie wordt de Dirac-deltafunctie δ(x-a) gedefinieerd door (vervang i door x en de sommatie over i door een integratie over x),
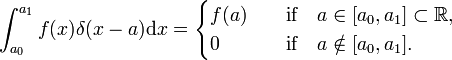
de Dirac-deltafunctie is geen gewone goed gedragende kaart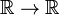 
, maar een distributie, ook bekend als een onjuiste of gegeneraliseerde functie. Natuurkundigen drukken zijn speciale karakter uit door te stellen dat de Dirac-deltafunctie alleen zin heeft als een factor in een integrand (“onder de integraal”)., Wiskundigen zeggen dat de deltafunctie een lineaire functie is op een ruimte van testfuncties.
inhoud
- 1 eigenschappen
- 2 Delta-convergente sequenties
- 2.1 Blokfuncties
- 2.2 Gaussiaanse functies
- 2.3 Lorentz-Cauchy-functies
- 2.4 Sinc-functies
- 3 derivaten van de delta-functie
- 3.,1 eigenschappen van de afgeleide
- 4 primitieve
- 5 de Dirac-deltafunctie in drie dimensies
- 6 Referenties
eigenschappen
meestal neemt men de onder-en bovengrens in de definitie van de deltafunctie gelijk aa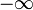n 
en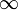 
, respectievelijk. Vanaf nu zal dit gebeuren.
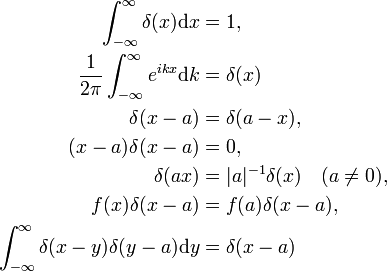
het bewijs van deze eigenschappen wordt geleverd door de juiste substituties in de integraal te maken en de gewone regels van de integrale calculus te gebruiken., De deltafunctie als fouriertransformatie van de eenheidsfunctie f(x) = 1 (de tweede eigenschap) wordt hieronder bewezen. De laatste eigenschap is de analogie van de vermenigvuldiging van twee identiteitsmatrices,
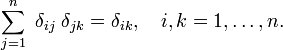
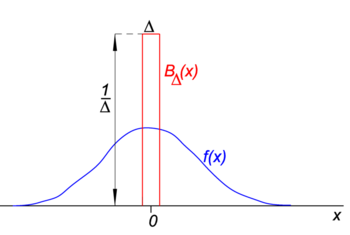
Fig. 1. Blok (“boxcar”) functie (rood) keer reguliere functie f (x) (Blauw).
Delta-convergente sequenties
Er bestaan families van reguliere functies Fa (x) waarvan de familieleden verschillen door de waarde van een enkele parameter α., Een voorbeeld van een dergelijke familie wordt gevormd door de familie van Gaussische functies Fa(x) = exp(−ax2), waarbij de verschillende waarden van de enkele parameter α de verschillende leden onderscheiden. Wanneer alle leden lineair normaliseerbaar zijn, d.w.z. de volgende integraal eindig is ongeacht α,
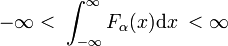
en alle leden een piek hebben rond x = 0, dan kan de familie een delta-convergente reeks vormen.,
Blokfuncties
het eenvoudigste voorbeeld van een delta-convergente reeks wordt gevormd door de familie van blokfuncties, gekenmerkt door positieve Δ,
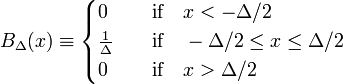
in Fig. 1 de blokfunctie BΔ wordt weergegeven in rood. Blijkbaar is de oppervlakte (breedte maal hoogte) onder de rode kromme gelijk aan eenheid, ongeacht de waarde van Δ,
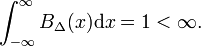
laat de willekeurige functie f(x) (Blauw in Fig. 1) zijn continu (geen sprongen) en eindig in de buurt van x=0., Wanneer Δ zeer klein wordt, en de blokfunctie zeer smal(en noodzakelijkerwijs zeer hoog omdat breedte maal hoogte constant is) wordt het product f(x) BΔ(x) in goede benadering gelijk aan f(0) BΔ (x). Hoe smaller het blok hoe beter de benadering., Dus ook voor de Δ gaat naar nul,
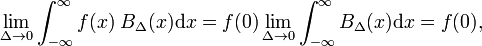
die kan worden vergeleken met de definitie van de delta-functie
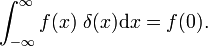
Dit toont aan dat de familie van functies blokkeren convergeert naar de Dirac delta functie voor het verminderen van de parameter Δ; het gezin vormt een delta-convergente reeks:
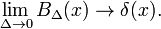
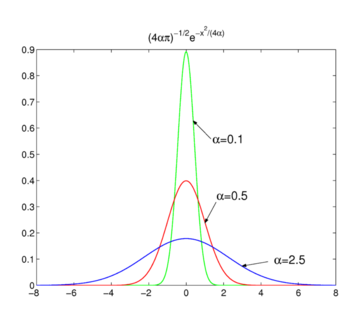
Afb. 2. Gaussiaanse functies.
opmerking: We geïntegreerd over de hele reële as., Uiteraard is dit niet nodig, we hadden de nulwaardigheidsvleugels van de blokfunctie kunnen uitsluiten en alleen over de bult in het midden kunnen integreren, van-Δ/2 tot +Δ/2. In wiskundige teksten, zoals bijvoorbeeld Ref. , deze verfijning van de integratiegrenzen is opgenomen in de definitie van de delta-convergente sequentie. Dat wil zeggen, het is vereist dat de integralen over de twee vleugels verdwijnen in de limiet. Omdat de delta-convergente sequenties in fysische toepassingen meestal aan deze voorwaarde voldoen, laten we de meer exacte wiskundige definitie weg.,
Gaussiaanse functies
beschouw de familie,
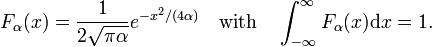
zoals weergegeven in Fig. 2 de functies pieken rond x = 0 en worden smaller voor het verminderen van α. Vandaar dat de familie van Gaussiaanse functies een delta-convergente reeks vormt,
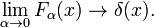
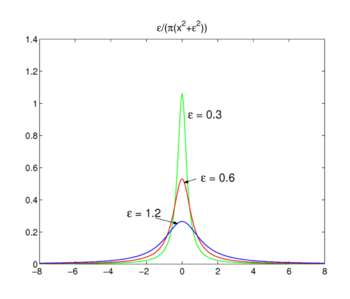
Fig. 3. Lorentz-Cauchy-functies
Lorentz-Cauchy-functies
de familie van functies weergegeven in Fig., 3
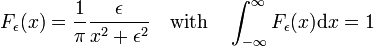
forms a delta-convergent sequence,
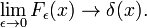
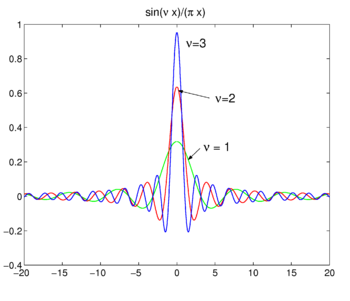
Fig. 4. Sinc functions.
Sinc functions
The family of functions (often called sinc functions) shown in Fig., 4 is
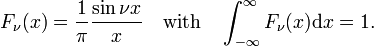
deze familie convergeert naar de deltafunctie voor het verhogen van ν
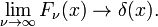
deze limiet leidt gemakkelijk tot de Fourier-integrale representatie van de deltafunctie:
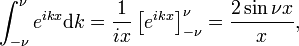
zodat
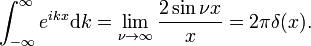
de Dirac-deltafunctie is de fouriertransformatie van de eenheidsfunctie f(x) = 1.
derivaten van de deltafunctie
beschouwen een differentieerbare functie f (x) die verdwijnt bij Plus en min oneindig.,d=”ed7dae11d6″>
Op dezelfde manier als een bewijst de omzet regel en Hermiticity van de quantum mechanische impuls operator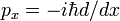 
we laten zien, dat d/dx is anti-Hermitian,
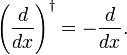
Inderdaad, wanneer we schrijven de integraal als een innerlijke product, dan volgt een gedeeltelijke integratie en het verdwijnen van f(x) over de integratie grenzen
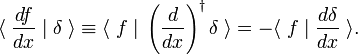
Deze omzet regel wordt gebruikt als de definitie van de afgeleide van de delta-functie
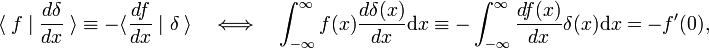
waar de eerste geeft aan dat de eerste afgeleide van f(x)., Volgens de definitie van de deltafunctie wordt de eerste afgeleide geëvalueerd in x = 0. Gebruikmakend van m maal de omzetregel, volgt hieruit dat het mth derivaat van de deltafunctie wordt gedefinieerd door
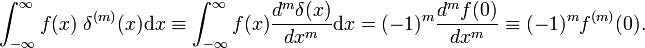
eigenschappen van het derivaat
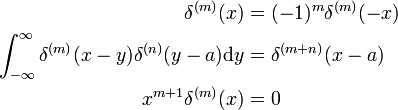
Deze resultaten kunnen worden aangetoond door de substitutie x → −x en het gebruik van de omzetregel voor d / dx (zie hierboven).,
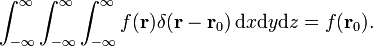
De drie-dimensionale delta functie kan worden factorized
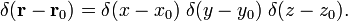
In sferische polaire coördinaten
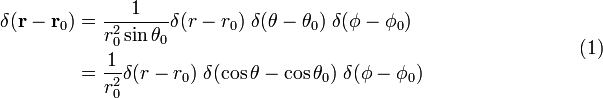
het Bewijs van formule (1)
Schrijf
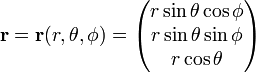
De Jacobian (Jacobi-determinant) van deze transformatie van Cartesische coördinaten naar de sferische poolcoördinaten is
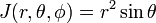
Overweeg
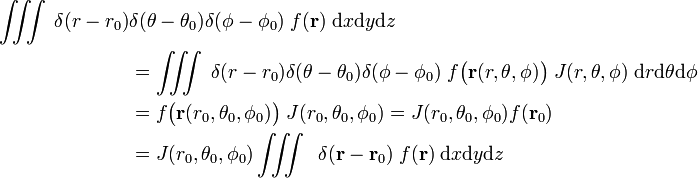
zodat
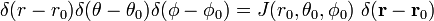
en
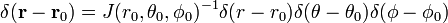
De laatste regel in vergelijking (1) volgt uit de kettingregel.,
De volgende nuttige en vaak toegepaste eigenschap wordt hier bewezen,
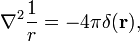
waarbij ∇2 de Laplace-operator is in driedimensionale Cartesiaanse coördinaten en r de lengte is van r.