dwarsdoorsnede

eigenschappen van oppervlakken

Centroid

het centroid van een vorm geeft het punt weer waaromheen het oppervlak van de doorsnede gelijkmatig is verdeeld. Als het gebied dubbel symmetrisch is over twee orthogonale Assen, ligt het centroïde op het snijpunt van die Assen. Als het gebied symmetrisch is over slechts één as, dan ligt het centroid ergens langs die as (de andere coördinaat moet worden berekend)., Als de exacte locatie van het zwaartepunt kan worden bepaald door middel van inspectie, het kan berekend worden door:

waar dA vertegenwoordigt het gebied van een infinitesimally klein onderdeel is van de totale oppervlakte van de doorsnede, en x en y zijn de coördinaten van het element dA met betrekking tot de as van belang.,

De centroidale locaties van gemeenschappelijke doorsneden zijn goed gedocumenteerd, dus het is meestal niet nodig om de locatie te berekenen met de vergelijkingen hierboven., van basic shapes waarvan centroidal locaties bekend zijn met betrekking tot een aantal referentie-punt, dan is de centroidal locatie van de samengestelde doorsnede kan worden berekend als:

waar xc,ik en yc,i zijn de rechthoekige coördinaten van de centroidal locatie van de i-de punt met betrekking tot het referentiepunt, en de Ai is het gebied van de i-de punt.,

Centroïdale afstand

De centroïdale afstand, c, is de afstand van het centroïd van een doorsnede tot de extreme vezel., De centroidal afstand in de y-richting voor een rechthoekige doorsnede is weergegeven in de figuur hieronder:

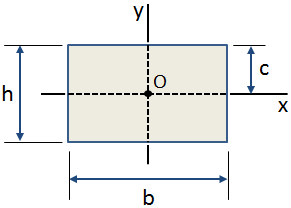
vaak gebruikt voor centroidal afstand zijn:

• het berekenen van de maximale bending spanningen in de doorsnede
• de berekening van de waarde van het eerste moment van het gebied, Q, boven een punt in de doorsnede te bepalen van de schuifspanning op dat punt

Eerste Moment van het Gebied

Het eerste moment van een ruimte met betrekking tot de as van de rente wordt als volgt berekend:

Qx = ∫ y dA

Qy = ∫ x dA

waar Qx is het eerste moment rond de x-as en Qy is het eerste moment over de y-as.,Als het gebied bestaat uit een verzameling van elementaire vormen, waarvan de centroidal locaties zijn bekend met betrekking tot de as van belang, dan is het eerste moment van de samengestelde gebied kan worden berekend als:

Merk op dat het eerste moment van het gebied wordt gebruikt bij de berekening van het zwaartepunt van de doorsnede met betrekking tot sommige oorsprong (zoals eerder besproken)., Het eerste moment wordt ook gebruikt bij het berekenen van de waarde van schuifspanning op een bepaald punt in de doorsnede. In dit geval wordt het eerste moment berekend voor een gebied dat een kleiner deel van de doorsnede vormt, waarbij het gebied wordt begrensd door het punt van belang en de extreme vezel (boven of onder) van de doorsnede. Het eerste moment wordt berekend over een as die door het midden van de doorsnede loopt.,

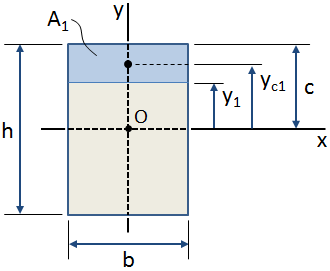
in de bovenstaande figuur is het gearceerde blauwe gebied het gebied van belang binnen de totale doorsnede.,nt van dit gebied met betrekking tot de x-as (die loopt door de doorsnede zwaartepunt, punt O in de bovenstaande figuur) wordt berekend als:

Als de centroidal locatie van het gebied van belang is bekend, dan is het eerste moment van het gebied met betrekking tot de as kan worden berekend als (zie de figuur hierboven):

Het moet worden opgemerkt dat het eerste moment van een gebied zal zijn, positief of negatief, afhankelijk van de positie van de positie van het gebied met betrekking tot de as van belang., Daarom zal het eerste moment van het gehele oppervlak van een doorsnede ten opzichte van zijn eigen centroid nul zijn.

Traagheidsmoment

het tweede traagheidsmoment van een dwarsdoorsnede, beter bekend als het traagheidsmoment I, is een indicatie van het vermogen van een constructiedeel om buiging te weerstaan.,(Noot 1) Ix en Iy zijn de traagheidsmomenten rond de x – en y – as, respectievelijk, en worden berekend door:

Ix = ∫ y2 dA

IY = ∫ x2 dA

waarbij x en y de coördinaten zijn van element dA ten opzichte van de as van rente.

meestal worden de traagheidsmomenten berekend ten opzichte van het middelpunt van de sectie. In dit geval worden ze aangeduid als centroidale traagheidsmomenten en worden aangeduid als Icx voor de traagheid rond de x-as en Icy voor de traagheid rond de y-as.,

De traagheidsmomenten van gemeenschappelijke doorsneden zijn goed gedocumenteerd, dus het is meestal niet nodig om ze te berekenen met de vergelijkingen hierboven. Eigenschappen van verschillende gemeenschappelijke doorsneden worden gegeven aan het einde van deze pagina.

als een doorsnede bestaat uit een verzameling basisvormen waarvan de centroïden allemaal samenvallen, dan is het traagheidsmoment van de samengestelde doorsnede gewoon de som van de individuele traagheidsmomenten. Een voorbeeld hiervan is een box balk die bestaat uit twee rechthoekige secties, zoals hieronder getoond., In dit geval heeft het buitenste gedeelte “positieve oppervlakte” en het binnenste gedeelte “negatieve oppervlakte”, dus het samengestelde traagheidsmoment is het aftrekken van het traagheidsmoment van het binnenste gedeelte van het buitenste gedeelte.

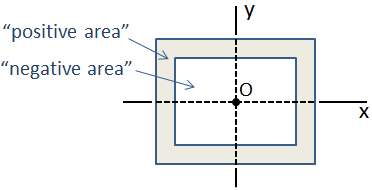
In het geval van een meer gecompliceerde samengestelde dwarsdoorsnede waarin de centroidale locaties niet samenvallen, kan het traagheidsmoment worden berekend met behulp van de stelling van de parallelle as.

Het is belangrijk om het traagheidsmoment van een gebied niet te verwarren met het massa traagheidsmoment van een vast lichaam., Het traagheidsmoment geeft de weerstand van een dwarsdoorsnede tegen buigen aan, terwijl het traagheidsmoment van de massa de weerstand van een lichaam tegen rotatie aangeeft.,

parallelle Asstelling

als het traagheidsmoment van een doorsnede over een centroidale as bekend is, dan kan de stelling van de parallelle as worden gebruikt om het traagheidsmoment over een parallelle as te berekenen:

waarbij Ic het traagheidsmoment over de centroidale AS is, d is de afstand tussen de centroidale as en de parallelle as, en A is het oppervlak van de doorsnede.,

als een dwarsdoorsnede bestaat uit een verzameling basisvormen waarvan de centroïdale traagheidsmomenten bekend zijn, samen met de afstanden van de centroïden tot een referentiepunt, dan kan de stelling van de parallelle as worden gebruikt om het traagheidsmoment van de samengestelde dwarsdoorsnede te berekenen.

bijvoorbeeld, een I-Beam kan benaderd worden door 3 rechthoeken, zoals hieronder getoond. Aangezien deze samengestelde sectie symmetrisch is over zowel de x – as als de y-as, kan het middelpunt van de sectie door inspectie op het snijpunt van die assen worden geplaatst. Het centroid bevindt zich aan de oorsprong, O, in de figuur.,

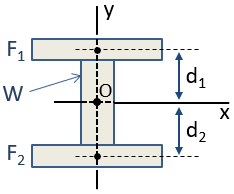
het traagheidsmoment van de samengestelde sectie kan worden berekend met behulp van de stelling van de parallelle as. Het centroïdale traagheidsmoment van de sectie rond de x-as, Icx, wordt berekend als:

waar de Icx-termen de traagheidsmomenten zijn van de afzonderlijke secties rond hun eigen centroïden in de oriëntatie van de x-as, zijn de D-termen de afstanden van de afzonderlijke sectiecentroïden tot de samengestelde sectiecentroïden, en de A-termen de gebieden van de afzonderlijke secties. Omdat de centroid van sectie W en de centroid van de samengestelde sectie samenvallen, is d nul voor die sectie en dus is er geen ad2 term.,

Het is belangrijk om de implicatie van de stelling van de parallelle as op te merken dat als een afzonderlijke sectie verder van het midden van de samengestelde sectie beweegt, de bijdrage van die sectie aan het traagheidsmoment van de samengestelde sectie toeneemt met een factor d2. Daarom, als de bedoeling is om het traagheidsmoment van een sectie over een bepaalde as te verhogen, is het het meest efficiënt om het gebied zo ver mogelijk van die as te lokaliseren. Dit verklaart de vorm van een I-balk., De flenzen zijn de belangrijkste bijdragers aan het traagheidsmoment, en het web dient om de flenzen van de buigende as te scheiden. Het web moet echter enige dikte behouden om knikken te voorkomen en omdat het web een aanzienlijk deel van de afschuifspanning in de sectie neemt.

polair Traagheidsmoment

het polair Traagheidsmoment I van een dwarsdoorsnede is een indicatie van het vermogen van een structureel element om torsie om een as loodrecht op de doorsnede te weerstaan., Het polaire Traagheidsmoment voor een sectie met betrekking tot een as kan worden berekend door:

waarbij x en y de coördinaten zijn van element dA met betrekking tot de as van belang, en r is de afstand tussen het element dA en de as van belang.,

hoewel het polaire Traagheidsmoment kan worden berekend met behulp van de bovenstaande vergelijking, is het meestal handiger om het te berekenen met behulp van de stelling van de loodrechte as, die stelt dat het polaire traagheidsmoment van een gebied de som is van de traagheidsmomenten over elke twee orthogonale assen die door de interesseas gaan:

midden van de doorsnede.,

Sectiemodulus

De maximale buigspanning in een bundel wordt berekend als σb = Mc / Ic, waarbij c de afstand is van de neutrale as tot de extreme vezel, Icis het centroïdale traagheidsmoment en M het buigmoment. De sectiemodulus combineert de termen c en Ic in de buigspanningsvergelijking:

met behulp van de sectiemodulus wordt de buigspanning berekend als σb = M / S. het nut van de sectiemodulus is dat deze de buigweerstand van een doorsnede in één term karakteriseert., Dit staat voor optimalisatie van de dwarsdoorsnede van een bundel toe om buiging te weerstaan door één enkele parameter te maximaliseren.

Draagradius

De draagradius is de afstand tot het middelpunt van een doorsnede waarop het gehele gebied kon worden geconcentreerd zonder enig effect te hebben op het traagheidsmoment.,>

A polar radius of gyration can also be calculated for problems involving torsion about a centroidal axis:

The rectangular radii of gyration can also be used to calculate the polar radius of gyration:

Eigenschappen van Gemeenschappelijke doorsneden

De tabel hieronder geeft de eigenschappen van gemeenschappelijke doorsnede. Meer uitgebreide tabellen zijn te vinden in de genoemde referenties.

De in de tabel berekende eigenschappen omvatten oppervlakte, centroidaal Traagheidsmoment, sectiemodulus en draagradius.,

Opmerkingen

Opmerking 1: de Doorbuiging van een Balk

De doorbuiging van een balk onder het buigen wordt bepaald door het traagheidsmoment van de doorsnede, de lengte van de straal, en de elasticiteitsmodulus van het materiaal. Meer details worden gegeven in deze bespreking van de afbuiging van de bundel.