de” eenheidscirkel ” is een cirkel met een straal van 1.
omdat het zo eenvoudig is, is het een geweldige manier om te leren en te praten over lengtes en hoeken.
het midden wordt op een grafiek gezet waar de x-as en de y-as elkaar kruisen, dus krijgen we deze nette opstelling hier.
sinus, cosinus en tangens
omdat de straal 1 is, kunnen we direct sinus, cosinus en tangens meten.,
Wat gebeurt er als de hoek θ 0°is?
cos 0° = 1, sin 0° = 0 en tan 0° = 0
Wat gebeurt er als θ 90°is?
cos 90° = 0, sin 90° = 1 en tan 90° is niet gedefinieerd
probeer het zelf!
probeer het eens!, Beweeg de muis om te zien hoe verschillende hoeken (in radialen of graden) invloed hebben op sinus, cosinus en raaklijn
De “zijden” kunnen positief of negatief zijn volgens de regels van cartesiaanse coördinaten. Dit maakt ook de sinus, cosinus en tangens verandering tussen positieve en negatieve waarden.
probeer ook de interactieve eenheidscirkel.,
Pythagoras
Pythagoras’ Stelling zegt dat voor een rechthoekige driehoek, het kwadraat van de lange zijde gelijk aan de som van de kwadraten van de twee andere zijden:
x2 + y2 = 12
Maar 12 is gewoon 1, dus:
x2 + y2 = 1
(de vergelijking van de eenheidscirkel)
Ook, omdat x=cos en y=sin, krijgen we:
(cos(θ))2 + (sin(θ))2 = 1
een handig “identiteit”
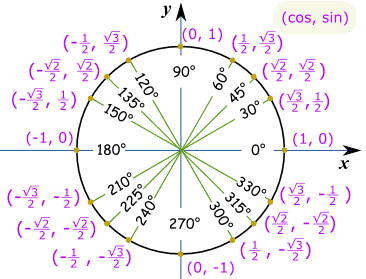
Belangrijk Hoeken: 30°, 45° en 60°
Je moet proberen te onthouden sin, cos en tan voor de hoeken van 30°, 45° en 60°.,
ja, ja, het is een pijn om dingen te onthouden, maar het zal het leven gemakkelijker maken als je ze kent, niet alleen in examens, maar andere momenten waarop je snelle schattingen moet doen, enz.
Dit zijn de waarden die u moet onthouden!,id=”0f47f3223b”>
What about tan?,
Goed, tan = sin/cos, dus kunnen we berekenen dit als volgt:
tan(30°) =sin(30°)cos(30°) = 1/2√3/2 = 1√3 = √33 *
tan(45°) =sin(45°)cos(45°) = √2/2√2/2 = 1
tan(60°) =sin(60°)cos(60°) = √3/21/2 = √3
* Opmerking: schrijven 1√3 kan kosten u merken (zie Rationele Noemers), zodat in plaats daarvan gebruik van √33
Snelle Schets
een Andere manier om u te helpen herinneren 30° en 60° is een snelle schets:
| Teken een driehoek met zijde een lengte van 2 | 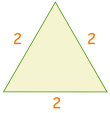 |
|
|
in tweeën Gesneden.,div id=”56c966b492″> Voorbeeld: sin(30°)Sine: sohcahtoa sinus is tegenover gedeeld door schuine zijde
sin(30°) = oppositehypotenuse = 12
De Hele CirkelVoor de hele cirkel die we moeten waarden in elk kwadrant, met de juiste plus-of min-teken, als per Cartesische Coördinaten: Merk op dat cos is in de eerste zonde is de tweede, dus het gaat (cos, sin):
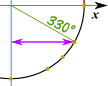
Opslaan als > PDF Voorbeeld: Wat is cos(330°) ?,
Maak een schets als deze, en we kunnen zien dat het de” lange ” waarde is: √32 en dit is dezelfde eenheidscirkel in radialen.
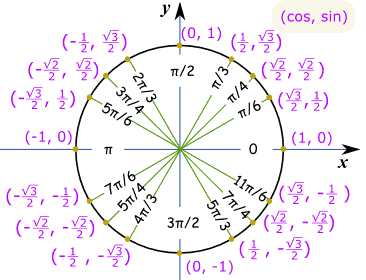
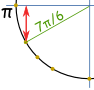
voorbeeld: Wat is sin(7π / 6) ?
denk “7π/6 = π + π/6”, maak dan een schets. We kunnen dan zien dat het negatief is en de “korte” waarde is − – ½ |