inhoud

constante acceleratie

We zijn allemaal bekend met het feit dat een auto versnelt wanneer we onze voet op het gaspedaal zetten. De snelheid van verandering van de snelheid van een deeltje met betrekking tot de tijd wordt zijn versnelling genoemd. Als de snelheid van het deeltje verandert met een constante snelheid, dan wordt deze snelheid de constante versnelling genoemd.,

bijvoorbeeld, als de snelheid van een deeltje dat zich in een rechte lijn beweegt gelijkmatig (bij een constante veranderingssnelheid) verandert van 2 m/s tot 5 m/s gedurende één seconde, dan is de constante versnelling 3 m/s\(^2\).

afnemende snelheid

als een deeltje een beginsnelheid heeft van 6 m / s en een constante versnelling van \(-2\) m/s\(^2\), dan:

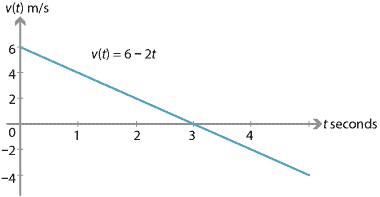
gedurende de eerste drie seconden neemt de snelheid van het deeltje af (het deeltje vertraagt). Na drie seconden rust het deeltje even., Na drie seconden neemt de snelheid nog steeds af, maar de snelheid neemt toe (het deeltje gaat steeds sneller).

samenvatting

als we aannemen dat de snelheid van verandering van snelheid (versnelling) een constante is, dan wordt de constante versnelling gegeven door

\

nauwkeuriger gezegd wordt de constante versnelling \(a\) gegeven door de formule

\

waarin \(v(t_i)\) de snelheid is op het moment \(t_i\). Omdat snelheid een vector is, is acceleratie ook een vector.,

de formules voor constante versnelling voor beweging in een rechte lijn

in dit gedeelte hebben we beweging in een rechte lijn met constante versnelling overwogen. Deze situatie is heel gebruikelijk; bijvoorbeeld, een lichaam dat beweegt onder invloed van zwaartekracht reist met een constante versnelling.

aangenomen wordt dat de beweging begint als \(t = 0\), en dat de beginpositie wordt ingenomen als de oorsprong, dat wil zeggen \(x(0) = 0\).,

De vijf vergelijkingen van beweging

1. \(v = u + at\)
2. \(x = \dfrac{(u+v)t}{2}\)
3. \(x = ut + \dfrac{1}{2}op^2\)
4. \(v^2 = r^2 + 2ax\)
5. \(x = vt – \dfrac{1}{2}op^2\)

Opmerking. Elk van de vijf vergelijkingen omvat vier van de vijf variabelen \(u, v, x, a, t\). Als de waarden van drie van de variabelen bekend zijn, dan kunnen de resterende waarden worden gevonden met behulp van twee van de vergelijkingen.,

afgeleid van de formules voor constante versnelling

de eerste bewegingsvergelijking

aangezien de versnelling constant is, hebben we \(a = \dfrac{v-u}{t}\). Dit geeft de eerste formule van beweging, \(v = u + bij\).

de tweede formule van beweging

de tweede vergelijking,

\

zegt dat verplaatsing wordt verkregen door het gemiddelde van de begin-en eindsnelheden te vermenigvuldigen met de tijd die tijdens de beweging is verstreken. Simpeler:

\

We kunnen deze vergelijking afleiden met behulp van het feit dat de verplaatsing gelijk is aan het ondertekende gebied onder de snelheid–tijd grafiek.,

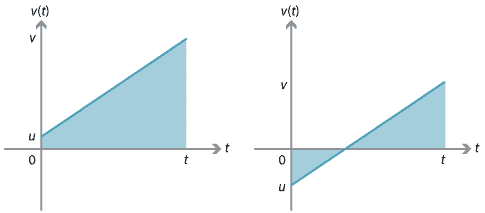
voor de grafiek rechts kan de verplaatsing worden gevonden door de twee driehoeken tussen de grafiek en de \(t\)-as Te beschouwen. Een van de driehoeken heeft een positief ondertekend gebied en de andere heeft een negatief ondertekend gebied.

het vinden van de verplaatsing van een deeltje uit de snelheid–tijd grafiek met behulp van integratie zal worden besproken in een later gedeelte van deze module.,

De derde vergelijking van de beweging

in plaats van \(v\) uit de eerste vergelijking in de tweede vergelijking geeft

\begin{align*}x &= \dfrac{(u+v)t}{2} \\ &= \dfrac{(u+u+at)t}{2} \\ &= \dfrac{2ut+op^2}{2} \\ &= ut + \dfrac{1}{2}op^2, \end{align*}

dat is de derde vergelijking. \(X\) is dus een kwadratisch getal in \(t\), en daarom is de grafiek van \(x\) tegen \(t\) een parabool.

de vierde bewegingsvergelijking

uit de eerste vergelijking hebben we \(t = \dfrac{v-u}{a}\)., Door dit te vervangen in de tweede vergelijking geeft

\begin{align*}x &= \dfrac{(u+v)t}{2} \\ &= \dfrac{(u+v)(v-u)}{2a} \\ &= \dfrac{v^2-U^2}{2A}. \ end{align*}

herschikken om \(v^2\) het onderwerp de vierde vergelijking te laten produceren: \(v^2 = u^2 + 2ax\).

de vijfde bewegingsvergelijking

vanaf de eerste vergelijking hebben we \(u = v-bij\)., Met de tweede vergelijking verkrijgen we

\begin{align*}x &= \dfrac{(u+v)t}{2} \\ &= \dfrac{(v-at+v)t}{2} \\ &= \dfrac{2vt-at^2}{2} \\ &= VT-\dfrac{1}{2}bij^2, \end{align*}

wat de vijfde vergelijking is.

verticale beweging

beweging door zwaartekracht is een goede context om het gebruik van de formules voor constante versnelling aan te tonen., Zoals eerder besproken, zijn onze twee richtingen in verticale beweging op en neer, en een beslissing moet worden genomen over welke van de twee richtingen positief is. Versnelling door zwaartekracht is een constante, met magnitude aangegeven door \(g\). In het volgende voorbeeld nemen we de richting naar boven om positief te zijn en nemen we \(g = 10\) m/s\(^2\).

verder gebruik van de bewegingsvergelijkingen

Next page – Content – Average velocity and average speed