eindige automaten kunnen outputs hebben die overeenkomen met elke overgang. Er zijn twee types eindige toestandsmachines die output genereren –
- Mealy Machine
- Moore machine
Mealy Machine
een Meal Machine is een FSM waarvan de output zowel van de huidige toestand als van de huidige invoer afhangt.,
het kan worden beschreven door een 6 tupel (Q,∑, O, δ, X, q0) waar −
-
Q Een eindige verzameling van toestanden is.
-
∑ is een eindige verzameling symbolen die het invoeralabet wordt genoemd.
-
O is een eindige verzameling symbolen die het uitvoeralabet wordt genoemd.
-
δ is de invoerovergangsfunctie waarbij δ: Q × → → Q
-
X is de uitvoerovergangsfunctie waarbij X: Q × → → O
-
q0 is de begintoestand van waaruit een input wordt verwerkt (q0 Q Q).,b424468″>
Output
The state diagram of the above Mealy Machine is −
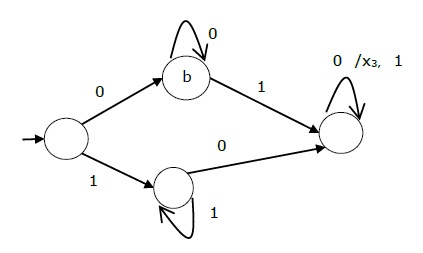
Moore Machine
Moore machine is an FSM whose outputs depend on only the present state.,
een Moore-machine kan worden beschreven door een 6 tupel (Q,∑, O, δ, X, q0) waar −
-
Q Een eindige verzameling van toestanden is.
-
∑ is een eindige verzameling symbolen die het invoeralabet wordt genoemd.
-
O is een eindige verzameling symbolen die het uitvoeralabet wordt genoemd.
-
δ is de invoerovergangsfunctie waar δ: Q × → → Q
-
X is de uitvoerovergangsfunctie waar X: Q → O
-
q0 is de begintoestand van waaruit een input wordt verwerkt (q0 ∈ Q).,iv>
Present state Next State Output Input = 0 Input = 1 → a b c x2 b b d x1 c c d x2 d d d x3 The state diagram of the above Moore Machine is −
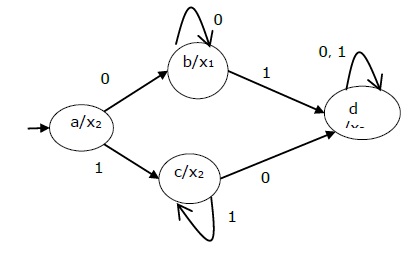
Mealy Machine vs., Moore Machine
de volgende tabel geeft een overzicht van de punten die een Meal Machine onderscheiden van een Moore Machine.
Mealy Machine Moore Machine uitvoer is alleen afhankelijk van de huidige toestand. over het algemeen heeft het minder toestanden dan Moore Machine. over het algemeen heeft het meer toestanden dan een Mealy Machine., de waarde van de uitvoerfunctie is een functie van de overgangen en de veranderingen, wanneer de invoerlogica op de huidige toestand wordt gedaan. de waarde van de outputfunctie is een functie van de huidige toestand en de veranderingen aan de klokranden, wanneer statuswijzigingen optreden. mely machines reageren sneller op ingangen. Ze reageren meestal in dezelfde klokcyclus. in Moore machines is meer logica nodig om de uitgangen te decoderen, wat resulteert in meer circuitvertragingen. Ze reageren meestal een klokcyclus later., Moore Machine to Mealy Machine
algoritme 4
Input − Moore Machine
Output − Mealy Machine
Stap 1 − Neem een lege Mealy Machine transitie tabel formaat.
Stap 2-Kopieer alle Moore Machinetoestanden naar dit tabelformaat.
Stap 3-Controleer de huidige toestanden en hun overeenkomstige uitgangen in de Moore Machine state table; als voor een toestand Qi output m is, kopieer deze dan in de uitvoerkolommen van de Mealy Machine state table waar Qi in de volgende toestand verschijnt.,der the following Moore machine −
Present State Next State Output a = 0 a = 1 → a d b 1 b a d 0 c c c 0 d b a 1 Now we apply Algorithm 4 to convert it to Mealy Machine.,8″>
Output
Mealy Machine to Moore Machine
Algorithm 5
Input − Mealy Machine
Output − Moore Machine
Step 1 − Calculate the number of different outputs for each state (Qi) that are available in the state table of the Mealy machine.,
Stap 2 – als alle uitgangen van Qi hetzelfde zijn, kopieer dan Qi. Als het n verschillende uitgangen heeft, breek Qi in n Staten als Qin waar n = 0, 1, 2…….
Stap 3 – als de uitgang van de begintoestand 1 is, voeg dan een nieuwe begintoestand aan het begin toe die 0 uitvoer geeft.,b424468″>
Output
Here, states ‘a’ and ‘d’ give only 1 and 0 outputs respectively, so we retain states ‘a’ and ‘d’., Maar de staten ‘ b ‘en’ c ‘ produceren verschillende outputs (1 en 0). Dus delen we b in b0, b1 en c in c0, c1.,”>
Output