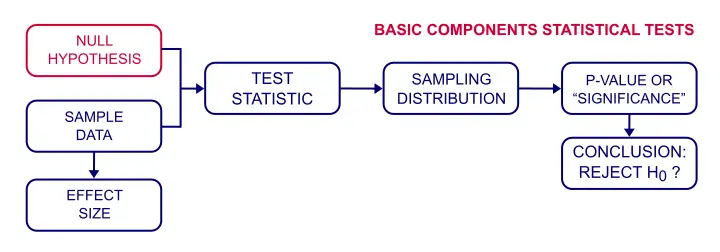
een nulhypothese is een precieze verklaring over een populatie die we proberen te verwerpen met steekproefgegevens.We geloven meestal niet dat onze nulhypothese (of H0) waar is. We hebben echter een exacte verklaring nodig als uitgangspunt voor statistische significantietesten.
nulhypothese voorbeelden
vaak-maar niet altijd – stelt de nulhypothese dat er geen associatie of verschil is tussen variabelen of subpopulaties., Zo zijn enkele typische nulhypothesen:
- De correlatie tussen frustratie en agressie is nul (correlatie-analyse);
- Het gemiddelde inkomen voor mannen is vergelijkbaar met dat Voor Vrouwen (onafhankelijke samples t-test);
- nationaliteit is (perfect) niet gerelateerd aan muziekvoorkeur (chi-kwadraat onafhankelijkheidstest);
- Het gemiddelde bevolkingsinkomen was gelijk over 2012 tot en met 2016 (herhaalde metingen ANOVA).
“Null” betekent niet “nul”
een veel voorkomend misverstand is dat “null” “nul”betekent. Dit is vaak, maar niet altijd het geval., Een nulhypothese kan bijvoorbeeld ook stellen dat de correlatie tussen frustratie en agressie 0.5.No nul erbij betrokken en – hoewel enigszins ongebruikelijk-volkomen geldig.
De “Nul” in “nulhypothese”is afgeleid van “nullify” 5: de nulhypothese is de stelling die we proberen te weerleggen, ongeacht of het (niet) een nuleffect specificeert.
nulhypothese Testing-Hoe werkt het?
Ik wil weten of geluk gerelateerd is aan rijkdom onder Nederlanders. Een benadering om dit uit te vinden is om een nulhypothese te formuleren., Omdat” verwant aan ” niet precies is, kiezen we de tegenovergestelde stelling als onze nulhypothese:de correlatie tussen rijkdom en geluk is nul bij alle Nederlanders.We zullen nu proberen deze hypothese te weerleggen om aan te tonen dat geluk en rijkdom met elkaar verbonden zijn.nu kunnen we redelijkerwijs niet alle 17.142.066 Nederlanders vragen hoe gelukkig ze zich over het algemeen voelen.

dus we zullen een voorbeeld (laten we zeggen, 100 mensen) vragen over hun rijkdom en hun geluk. De correlatie tussen geluk en rijkdom blijkt 0,25 in onze steekproef te zijn., Nu hebben we één probleem: de resultaten van de steekproef verschillen enigszins van de resultaten van de populatie. Dus als de correlatie echt nul is in onze populatie, kunnen we een niet-nul correlatie vinden in onze steekproef. Om dit belangrijke punt te illustreren, neem een kijkje op de scatterplot hieronder. Het visualiseert een nul correlatie tussen geluk en rijkdom voor een hele bevolking van n = 200.

nu trekken we een willekeurige steekproef van N = 20 uit deze populatie (de rode stippen in ons vorige scatterplot). Hoewel onze populatie correlatie nul is, vonden we een duizelingwekkende 0.,82 correlatie in ons monster. De onderstaande figuur illustreert dit door alle niet-bemonsterde eenheden uit ons vorige verstrooiingsschema weg te laten.

Dit roept de vraag op hoe we ooit iets over onze populatie kunnen zeggen als we er maar een kleine steekproef van hebben. Het basis antwoord: We kunnen zelden iets zeggen met 100% zekerheid. We kunnen echter veel zeggen met 99%, 95% of 90% zekerheid.
kans
dus hoe werkt dat? Sommige resultaten zijn hoogst onwaarschijnlijk gezien onze nulhypothese., Zo toont de figuur hieronder de waarschijnlijkheid voor verschillende steekproefcorrelaties (n = 100) als de populatiecorrelatie werkelijk nul is.

een computer kan deze waarschijnlijkheden gemakkelijk berekenen. Hiervoor is echter een steekproefgrootte (100 in ons geval) en een veronderstelde populatiecorrelatie ρ (0 in ons geval) vereist. Daarom hebben we een nulhypothese nodig.
als we deze sampling distributie zorgvuldig bekijken, zien we dat sample correlaties rond 0 het meest waarschijnlijk zijn: er is een 0.68 kans op het vinden van een correlatie tussen -0.1 en 0.1. Wat betekent dat?, Denk eraan dat waarschijnlijkheden kunnen worden gezien als relatieve frequenties. Stel je voor dat we 1000 monsters zouden nemen in plaats van degene die we hebben. Dit zou resulteren in 1.000 correlatiecoëfficiënten en ongeveer 680 daarvan-een relatieve frequentie van 0,68 – zouden in het bereik -0,1 tot 0,1 liggen. Ook is er een 0.95 (of 95%) kans op het vinden van een steekproef correlatie tussen -0,2 en 0,2.
P-waarden
We vonden een monstercorrelatie van 0,25. Hoe waarschijnlijk is dat als de populatie correlatie nul is?, Het antwoord is bekend als de p-waarde (kort voor kanswaarde): een p-waarde is de kans op het vinden van een of andere steekproefuitkomst of een meer extreme als de nulhypothese waar is.Gezien onze 0.25 correlatie betekent” extremer ” meestal groter dan 0.25 of kleiner dan -0.25. We kunnen het niet zien aan onze grafiek, maar de onderliggende tabel vertelt ons dat p ≈ 0,012. Als de nulhypothese waar is, is er een kans van 1,2% op het vinden van onze steekproef correlatie.
conclusie?
als onze populatiecorrelatie werkelijk nul is, dan kunnen we een steekproefcorrelatie van 0,25 vinden in een steekproef van n = 100., De kans dat dit gebeurt is slechts 0,012 dus het is zeer onwaarschijnlijk. Een redelijke conclusie is dat onze populatie correlatie toch niet nul was.conclusie: we verwerpen de nulhypothese. Gezien onze steekproefuitkomst, geloven we niet langer dat geluk en rijkdom niets met elkaar te maken hebben. We kunnen dit echter nog steeds niet met zekerheid zeggen.
nulhypothese-beperkingen
tot nu toe hebben we alleen geconcludeerd dat de populatiecorrelatie waarschijnlijk niet nul is. Dat is de enige conclusie van onze nulhypothese benadering en het is niet echt interessant.,wat we echt willen weten is de populatie correlatie. Onze steekproef correlatie van 0,25 lijkt een redelijke schatting. We noemen zo ‘ n enkel getal een puntschatting.
nu kan een nieuw monster met een andere correlatie komen. Een interessante vraag is hoeveel Onze Sample correlaties zouden fluctueren ten opzichte van samples als we er veel zouden tekenen. De figuur hieronder toont precies dat, uitgaande van onze steekproefgrootte van n = 100 en onze (punt) schatting van 0,25 voor de populatie correlatie.,

betrouwbaarheidsintervallen
ons resultaat van de steekproef suggereert dat ongeveer 95% van de vele monsters een correlatie tussen 0,06 en 0,43 zou moeten hebben. Dit bereik wordt een betrouwbaarheidsinterval genoemd. Hoewel niet precies correct, het is het meest gemakkelijk al van als de bandbreedte die waarschijnlijk de populatie correlatie omsluiten.
Een ding om op te merken is dat het tijdsinterval vrij breed is. Het bevat bijna een nulcorrelatie, precies de nulhypothese die we eerder verwierpen.,
Een ander ding om op te merken is dat onze sampling distributie en betrouwbaarheidsinterval enigszins asymmetrisch zijn. Ze zijn symmetrisch voor de meeste andere statistieken (zoals middelen of beta-coëfficiënten), maar niet correlaties.