sneeuw bij temperaturen boven het vriespunt

heeft u zich ooit afgevraagd hoe het kan sneeuwen bij temperaturen boven het vriespunt? Nou, de naïeve verklaring is dat het gewoon tijd kost voor de sneeuwvlokken te smelten zodra ze doordringen boven ijskoude lucht, als ze afdalen naar beneden naar de grond. Dit is natuurlijk de reden waarom hagel kan vallen bij warm weer. Hagelstenen vallen gewoon snel, te snel om de warme lucht de hagel te laten smelten. Dit is echter niet de belangrijkste verklaring voor waarom het kan sneeuwen als het boven het vriespunt is.,
uit onderstaande figuur blijkt dat er een duidelijke afhankelijkheid is van de vochtigheid – hoe droger het is, hoe warmer het kan zijn tijdens het sneeuwen. Dit houdt in dat de belangrijkste factor, althans in droge omstandigheden, te maken heeft met vochtigheid. En deze factor is verdamping. Meer specifiek, als de sneeuwvlokken dalen, verdampen ze. Dit proces neemt warmte en houdt de vlokken koud.
dus, als we de maximale temperatuur willen berekenen, moeten we schatten naar de netto warmtebalans van de vlok. Ten eerste, als de vlokken reizen in een warme omgeving, krijgen ze warmte uit de omgeving door geleiding., Ten tweede wordt warmte gebruikt om de vlokken te verdampen, waardoor ze worden afgekoeld. Als de verdampingswarmte “sink” groter is dan de warmtegeleiding, blijven de vlokken bevroren.
Het blijkt dat dit gemakkelijk kan worden berekend. Nee, Het is niet eenvoudig om de warmtegeleiding of de verdampingswarmte te berekenen, maar de verhouding wel, omdat verschillende Onbekende geometrische factoren elkaar opheffen.
als je niet geeft om de berekening (omdat je geen science freak bent), kun je gewoon de rekenmachine pagina bezoeken.
als het je iets kan schelen, hier is de afleiding., Stel dat de stroming rond de vlokken zodanig is dat er een grenslaag van breedte d omheen ontstaat. De totale warmtestroom $F_H$ naar de vlok (bijv. J/sec in MKS) wordt gegeven door de wet van Fourier:

waarbij $\kappa$ de warmtediffusiecoëfficiënt van lucht is (bijv. m2/sec in MKS), c is de warmtecapaciteit van lucht (J/kg in MKS), A is de oppervlakte van de grenslaag rond de vlok, terwijl δt het temperatuurverschil is tussen de VLOK en de omgeving., op dezelfde manier kan men de wet van Fick gebruiken om de diffusie van waterdamp te verkrijgen van de vlok (waar de temperatuur bijna bevriest en de relatieve vochtigheid 100% is) naar de omgeving, waar de temperatuur hoger is en de relatieve vochtigheid lager:

$$ \Phi_W \approx D A {\Delta \rho_W \over d}. hier is D de waterdiffusiecoëfficiënt (b.v. m2/sec in MKS) en ρ de waterdampdichtheid (kg/m3 in MKS)., het verdampende ijs vereist warmte, dus als er een waterdamp massa flux van Φ uit de vlok is, zou het warmte nodig hebben met een snelheid van $F_w = \epsilon \Phi$ waar $\epsilon$ de warmte van de verdamping van ijs is (J / kg in MKS).
de hoogste temperatuur waarboven de sneeuwvlok smelt, is de temperatuur waarvoor de twee warmtestromen gelijk zijn:

$$ F_w = F_H ~~\rightarrow ~ ~ \ Epsilon D \ Delta {\rho_w\over d} A = {\Kappa a \ Over c} {\Delta T_ {max} \over d}.$ $

merk op dat de geometrie van de stroom rond de vlok wegvalt, omdat beide warmtefluxen op dezelfde manier afhankelijk zijn van d en A., Dit zou ook het geval zijn als de grenslaag rond de vlok zo complex is dat d eigenlijk afhangt van de richting. Vandaar dat

$$ \ Delta T_ {max} = c \Epsilon {D \over \kappa} \ Delta \ rho = c \Epsilon {D \over \kappa} \ Delta (\rho_{sat} RH).$$

waarbij $ \ rho_{sat}$ de verzadiging waterdampdichtheid is.
het inpluggen van de getallen (die bijvoorbeeld te vinden zijn in het CRC handbook of chemistry and physics) resulteert in een impliciete vergelijking voor de temperatuur, omdat de verzadigingsdichtheid van waterdamp ook afhankelijk is van de temperatuur., We kunnen de zaken vereenvoudigen als we in plaats daarvan vragen wat de relatieve vochtigheid is die nodig is om de vlok bevroren te houden bij een bepaalde temperatuur. Het is:

$ $ RH = 9.5 \ exp \ left (- 17.27 T_C \ over T_C + 238.3^ \ circ \ right) \left( 10.5^\circ\mathrm{C} – t_c\right)\%.$ $

waarbij $T_C$ de temperatuur is in graden Celsius.
Deze functie kan worden gezien in de onderstaande figuur, samen met gegevens uit Matsuo en Sasyo, 1981. Zoals uit de figuur blijkt, is de berekende grafiek ongeveer de ondergrens waaronder er helemaal geen regen valt. Bij warmere temperaturen is er een mix., Tot ongeveer 1°C boven de no smeltlijn, is er meestal sneeuw terwijl tussen ongeveer 1°C en 2°C boven de lijn, is het meestal regen, maar sneeuw is mogelijk. Deze gebeurtenissen kunnen te wijten zijn aan extra effecten, zoals sterke downdraft, tijd die nodig is om de sneeuw te smelten, enz.

sneeuw of regen? De rode lijn is de niet-smeltende lijn. Daaronder koelen sneeuwvlokken door verdamping meer af dan ze uit de omgeving verwarmen, waardoor ze bevroren blijven. De magneta en blauwe lijnen liggen +1°C en +2°C boven de no smeltlijnen., Tussen 0°C en +1°C boven de no smeltlijn sneeuwt het meestal terwijl het meestal regent tussen +1°C en +2°C boven de no smeltlijn. Bij warmere temperaturen regent het. De groene datapunten zijn gebeurtenissen verzameld door Matsuo en Sasyo (1981) in Wajima Japan, tussen 1975 en 1978.

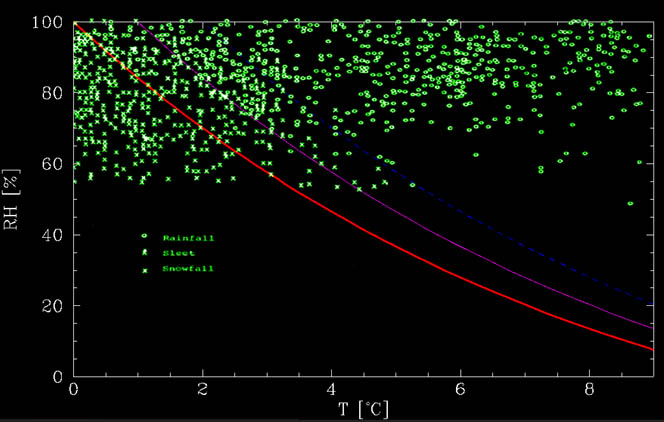
als we Warme Sneeuw willen waarnemen, zijn zeer droge omstandigheden vereist. Bijvoorbeeld, als de grondvochtigheid is slechts ongeveer 20% (zeer zeldzaam, want als er Neerslag, de atmosfeer is over het algemeen nat!) dan kan het sneeuwen bij 8°C (of 46°F voor Engelse gebruikers).,
Een andere eis is dat de lucht nergens langs de afdaling de no smeltlijn overschrijdt. Als dat zo is, zal de vlok natuurlijk smelten.
als de temperatuur boven het vriespunt uitstijgt, zijn er geen parameters waarmee het type neerslag met zekerheid kan worden bepaald. Het enige wat we dan kunnen voorspellen is de kans dat er daadwerkelijk sneeuw valt. Dit kan worden gedaan met behulp van de resultaten van Häggmark en Ivarsson (1997), alleen gecorrigeerd om de bevroren-bol te gebruiken en niet de natte-bol temperatuur.
De bottom line is een calculator waarmee de kans op sneeuw kan worden geschat.,

Hoe is het gerelateerd aan de natte boltemperatuur? De relatie tussen de temperatuur die we vinden en de vriestemperatuur van water is zeer vergelijkbaar met de relatie tussen droge bol en web bol temperaturen (waarbij de laatste is de gereduceerde temperatuur een natte thermometer zal lezen als gevolg van water verdamping). Het belangrijkste verschil is dat natte bol temperatuur omvat verdamping van water, terwijl in ons geval, het is verdamping van ijs, met 15% meer energieverlies. We zijn dus in wezen op zoek naar de droge boltemperatuur waarvoor de” bevroren ” boltemperatuur 0°C is.