Zoek alle wortels van een Veeltermfunctie
gebruik vpasolve om alle oplossingen voor de functie f(x)=6×7-2×6+3×3-8 te vinden.
syms f(x)f(x) = 6*x^7-2*x^6+3*x^3-8;sol = vpasolve(f)
vpasolvegeeft zeven wortels van de functie terug, zoals verwacht, omdat de functie een veelterm van graad zeven is.,
zoek nullen van een niet-polynomiale functie met behulp van zoekbereiken en beginpunten
een plot van de functie f(x)=e(x / 7)cos(2x) toont periodieke nullen, waarbij de hellingen op de nulpunten toenemen naarmate x toeneemt.
syms xh = fplot(exp(x/7)*cos(2*x),);grid on
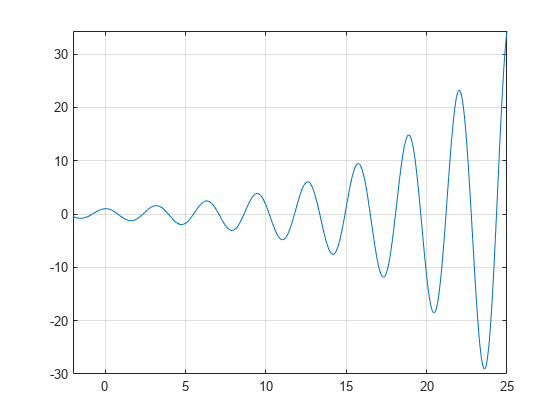
gebruik vpasolveom een nul van de functief. Merk op dat vpasolve slechts één oplossing van een niet-polynomiale vergelijking geeft, zelfs als er meerdere oplossingen bestaan., On repeated calls, vpasolve returns the same result.
f = exp(x/7)*cos(2*x);for k = 1:3 vpasolve(f,x)end
ans = -7.0685834705770347865409476123789-vpa('7.0685834705770347865409476123789')
ans = -7.0685834705770347865409476123789-vpa('7.0685834705770347865409476123789')
ans = -7.0685834705770347865409476123789-vpa('7.0685834705770347865409476123789')
To find multiple solutions, set the option 'Random' to true. This makes vpasolve choose starting points randomly., For information on the algorithm that chooses random starting points, see Algorithms on the vpasolve page.
for k = 1:3 vpasolve(f,x,'Random',true)end
ans = -226.98006922186256147892598444194-vpa('226.98006922186256147892598444194')
ans = 98.174770424681038701957605727484vpa('98.174770424681038701957605727484')
ans = 52.621676947629036744249276669932vpa('52.621676947629036744249276669932')
To find a zero close to x=10, set the starting point to 10.,
vpasolve(f,x,10)
ans = 10.210176124166828025003590995658vpa('10.210176124166828025003590995658')
om de nul te vinden in de buurt van x=1000, zet het beginpunt op 1000.
vpasolve(f,x,1000)
ans = 999.8118620049516981407362567287vpa('999.8118620049516981407362567287')
om de nul in het bereik 15≤x≤25 te vinden, Stel het zoekbereik in op .,
vpasolve(f,x,)
ans = 21.205750411731104359622842837137vpa('21.205750411731104359622842837137')
om meerdere nullen te vinden in het bereik , u kuntvpasolveniet herhaaldelijk aanroepen omdat het hetzelfde resultaat geeft bij elke oproep, zoals eerder getoond. Stel in plaats daarvan het zoekbereik in en stel 'Random' in op true.,
for k = 1:3 vpasolve(f,x,,'Random',true)end
ans = 21.205750411731104359622842837137vpa('21.205750411731104359622842837137')
ans = 21.205750411731104359622842837137vpa('21.205750411731104359622842837137')
ans = 16.493361431346414501928877762217vpa('16.493361431346414501928877762217')
Omdat 'Random' selecteert uitgangspunten willekeurig, dezelfde oplossing kan worden gevonden op de opeenvolgende gesprekken.,
Zoek alle nullen in een opgegeven zoekbereik
Creëer een functie findzeros om systematisch alle nullen voor f in een bepaald zoekbereik te vinden, binnen een opgegeven fouttolerantie. De functie begint met het invoerzoekbereik en roept vpasolve aan om een nul te vinden. Vervolgens splitst het het zoekbereik in twee rond de nulwaarde en roept zichzelf recursief aan met de nieuwe zoekbereiken als ingangen om meer nullen te vinden.
De functie wordt hier sectie voor sectie uitgelegd.,
Declareer de functie met de drie ingangen en één uitgang. De eerste ingang is de functie, de tweede ingang is het bereik, en de optionele derde ingang kunt u de fout tussen een nul en de hogere en lagere grenzen gegenereerd uit het specificeren.
function sol = findzeros(f,range,err)
Als u het optionele argument voor fouttolerantie niet opgeeft, findzeros stelt err in tot 0.001.
if nargin < 2 err = 1e-3;end
zoek een nul in het zoekbereik met vpasolve.,
sol = vpasolve(f,range);
als vpasolve geen nul, uitgang vindt.
if(isempty(sol)) return
als vpasolve een nul vindt, splitst u het zoekbereik op in twee zoekbereiken boven en onder de nul.
else lowLimit = sol-err; highLimit = sol+err;
aanroep findzeros met het lagere zoekbereik. Als findzeros nullen retourneert, kopieer de waarden in de solution array en sorteer ze.
temp = findzeros(f,,1); if ~isempty(temp) sol = sort(); end
aanroep findzeros met het hogere zoekbereik., Als findzeros nullen retourneert, kopieer de waarden in de solution array en sorteer ze.
temp = findzeros(f,,1); if ~isempty(temp) sol = sort(); end returnendend
de gehele functie findzeros is als volgt. Sla deze functie op als findzeros.m in de huidige map.
syms f(x)f(x) = exp(x/7)*cos(2*x);sol = findzeros(f,)'
verkrijg oplossingen met willekeurige precisie
gebruik digits om de precisie in te stellen van de oplossingen die door vpasolveworden geretourneerd., Standaard geeft vpasolve oplossingen terug met een nauwkeurigheid van 32 significante cijfers.
f = exp(x/7)*cos(2*x);vpasolve(f)
ans = -7.0685834705770347865409476123789-vpa('7.0685834705770347865409476123789')
gebruik digitsom de precisie te verhogen tot 64 significante cijfers. Als u digits wijzigt, moet u ervoor zorgen dat u de huidige waarde opslaat zodat u deze kunt herstellen.,
digitsOld = digits;digits(64)vpasolve(f)
ans = -7.068583470577034786540947612378881489443631148593988097193625333-vpa('7.068583470577034786540947612378881489443631148593988097193625333')
verander vervolgens de precisie van de oplossingen naar 16 significante cijfers.
digits(16)
Los Multivariate vergelijkingen op met behulp van zoekbereiken
overweeg het volgende stelsel van vergelijkingen.
z = 10 (cos(x)+cos (y))z=x+y2-0.1x2yx+y-2.7=0
een grafiek van de vergelijkingen voor 0≤x≤2,5 en 0≤x≤2,5 laat zien dat de drie oppervlakken elkaar snijden in twee punten., Gebruik viewom de plot beter te visualiseren. Gebruik caxisom de kleurenkaartwaarden te schalen.
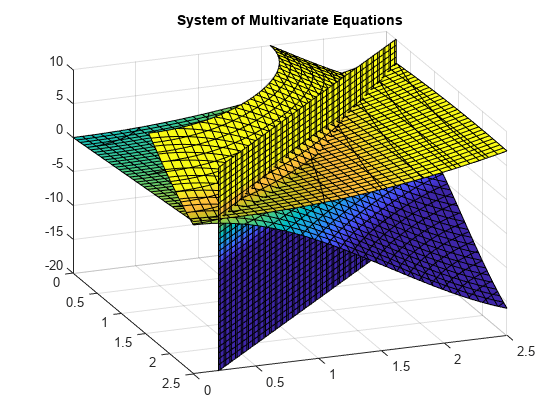
gebruik vpasolve om een punt te vinden waar de oppervlakken elkaar kruisen. De functie vpasolve geeft een structuur terug. Om toegang te krijgen tot de x-, y-, en z-waarden van de oplossing, indexeer in de structuur.,
sol = vpasolve(equations);
om een gebied van de oplossingsruimte te zoeken, specificeer zoekbereiken voor de variabelen. Als u de bereiken 0≤x≤1.5 en 1.5≤y≤2.5 opgeeft, dan zoekt de functie vpasolve in het getoonde begrensd gebied.

gebruik vpasolve om een oplossing voor dit zoekbereik te vinden. Om een zoekbereik voor z weg te laten, stelt u het derde zoekbereik in op .,
vars = ;range = ;sol = vpasolve(equations, vars, range);
om meerdere oplossingen te vinden, stelt u de optie 'Random'in optrue. Dit zorgt ervoor dat vpasolve willekeurige beginpunten gebruikt bij opeenvolgende runs. De optie 'Random' kan in combinatie met zoekbereiken worden gebruikt om vpasolve willekeurige beginpunten binnen een zoekbereik te laten gebruiken. Omdat 'Random' willekeurig startpunten selecteert, kan dezelfde oplossing gevonden worden bij opeenvolgende aanroepen., Roep vpasolve herhaaldelijk aan om er zeker van te zijn dat u beide oplossingen vindt.
Plot de vergelijkingen. Leg de oplossingen over elkaar als een spreidingsdiagram van punten met geel X markers met scatter3. Om de plot beter te visualiseren, maakt u twee oppervlakken transparant met alpha. Schalen van de kleurenkaart naar de plotwaarden met caxis, en verander het perspectief met view.
vpasolve vindt oplossingen op het snijpunt van de oppervlakken gevormd door de vergelijkingen zoals getoond.,

Lastly, restore the old value of digits for further calculations.
digits(digitsOld)