op deze pagina ‘ s kijken we naar enkele interessante concepten, we kijken naar gebogen ruimte: wat gebogen ruimte betekent, hoe we kunnen zien of een ruimte van binnen of Van buiten is gebogen.
we bekijken hoe we het type ruimte in een andere ruimte kunnen insluiten en zien dat we verschillende ruimtes op verschillende manieren kunnen in kaart brengen.
we kijken ook naar verdichting en hoe we oneindig grote en infinitesimaal kleine vectoren in onze ruimtes kunnen representeren op manieren die niet leiden tot singulariteiten en andere problemen.,
deze concepten blijken nuttig te zijn, zelfs als we met een vlakke ruimte werken, zullen we manieren vinden om vectoren en vlakken weer te geven die niet door de oorsprong gaan. Dit geeft ons manieren om rotaties en vertalingen te vertegenwoordigen als een enkele operatie.
de andere toepassing is relativistische ruimte-tijd.
Rienmanniaanse meetkunde
in de rienmanniaanse meetkunde kan de ruimte op verschillende plaatsen krommen (zie variëteiten) hier kijken we naar meetkunden waar de kromme van de ruimte constant is.,
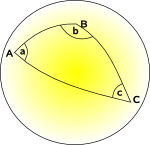
Eulidean Geometrie
vlakke ruimte
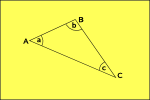
Hyperbolische Geometrie
de ruimte krommen naar buiten
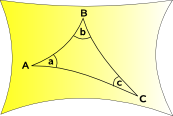
Sferische Geometrie en de Elliptische Meetkunde
de ruimte naar binnen buigt
In een gebogen (Niet-Euclidische) meetkunde wij niet kunnen vinden van een set coördinaten die onderling loodrecht op elkaar staan, waar het coördineren lijnen zijn allemaal parallel aan elkaar en waar elk vierkant heeft hetzelfde gebied., We kunnen misschien een coördinatenstelsel vinden waar we sommige van deze kunnen doen, maar niet allemaal.
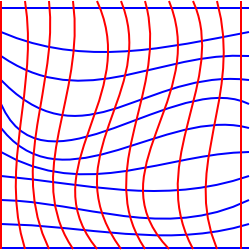
dit diagram probeert deze situatie in 2 dimensies te illustreren, hoewel het een beetje misleidend is, omdat we het op een vlak hebben getekend zodat we rechthoekige coördinaten hadden kunnen tekenen.
om een situatie te illustreren waarin dit onmogelijk is, kunnen we denken aan een tweedimensionaal vlak dat is uitgerekt tot de derde dimensie.,

in deze situatie kunnen we coördinaten kiezen die een rechthoekig raster vormen wanneer ze geprojecteerd worden op een horizontaal vlak, maar voor een persoon die in het oppervlak leeft, zullen sommige rastervierkantjes een groter gebied lijken te hebben dan andere en zullen de rasterlijnen mogelijk niet parallel lijken te zijn. Er is geen tweedimensionaal coördinatenstelsel dat parallelle lijnen, hoeken en gebieden tegelijkertijd zal behouden.,
een soortgelijk voorbeeld probeert het aardoppervlak in kaart te brengen, we kunnen breedtegraad-en lengtegraadlijnen gebruiken, maar de lengtegraadlijnen komen dichter bij de Polen.
in deze gevallen kunnen we werken in termen van 3 dimensionale coördinaten en dat is een benadering die we zullen nemen met sommige soorten niet-Euclidische geometrieën. Het is vaak mogelijk om een bepaalde meetkunde in een hogere dimensionale meetkunde in te bedden om deze meer Euclidisch te maken.,
het is soms het geval dat een meetkunde op grote schaal niet-Euclidisch is, maar als we er op steeds kleinere schaal naar kijken, dan benadert het een Euclidische meetkunde. Om dit te doen moeten we een coördinatenstelsel vinden waar hoeken op elk punt behouden blijven, dat wil zeggen dat de horizontale en verticale coördinatenlijnen altijd bij 90° moeten snijden, ook al zijn de lijnen niet recht. Dit staat bekend als een hoekgetrouwe meetkunde. In dit type meetkunde kunnen we op zijn minst een lokaal coördinatenstelsel definiëren.,
gerelateerd aan dit is of de geometrie kan worden gedifferentieerd en geïntegreerd, een voorwaarde hiervoor is dat het goed gedragen moet zijn en geen plotselinge sprongen moet hebben etc. Sommige geometrieën en coördinatenstelsels kunnen goed gedragen op sommige plaatsen, maar hebben singulariteiten etc.
voor een discussie over hoe kromming wordt gemeten, zie deze pagina.
wiskundige notatie
Hoe gaan we om met geometrieën waarbij we niet alle regels kunnen gebruiken die van toepassing zijn op de Euclidische meetkunde?,
een benadering is het gebruik van tensor notatie, dit biedt conventies en notatie die ons helpen bij het schakelen tussen verschillende coördinatenstelsels. Een orthogonaal coördinatenstelsel, lokaal tot elk punt, kan worden gedefinieerd door basisvectoren te gebruiken die raaklijnen zijn aan de coördinatenlijnen.,Spruitstuk
zie deze pagina
de Relatie tussen Hyperbolische en Minkowski Geometrie
| Minkowski Geometrie | Hyperbolische Geometrie | |
| punt | gebeurtenis in ruimte-tijd | deeltje in uniform motion |
| afstand tussen twee punten | ruimte-tijd interval tussen twee gebeurtenissen | relatieve snelheid tussen twee van dergelijke deeltjes |
Terminologie
Hier kijken we naar de terminologie zoals geometrie, spaties, maquettes, projecties en transformeert., Het is heel moeilijk als we beginnen met niet-Euclidische meetkunden, omdat we dezelfde terminologie gebruiken als we gewend zijn in de conventionele Euclidische ruimte, maar de termen kunnen iets andere eigenschappen hebben.,probeer
Elliptische Meetkunde
Modellen
Voorbeelden zijn:
- Bovenste helft-vlak model
- Poincaré-schijf model
- Projectieve model
- Conformele model
Projecties
Stereografische Projectie
Transformeert
Invariant
Voorbeelden zijn:
- Möbius Transformatie
- Lorentz Transformatie
Parallel Postulaat
Als we weg te nemen de parallelle postulaat van de Euclidische Ruimte.,
Dit leidt tot:
- parallel postulaat is onwaar
- de hoeken van een driehoek voegen niet toe aan π
- voor een vorm van een bepaalde grootte bestaat er in het algemeen geen vergelijkbare vorm van een grotere grootte.,l ste l l ing
conformele (Poincaré-schijf ) rechte lijnen geodesics segmenten van cirkels hoek behoud meer interne hoeken van de driehoek π-(α+β+γ)=CΔ afstand tussen twee punten met