låt oss börja med ett enkelt exempel, säg att vi vill multiplicera ut (2x-3)3. Detta skulle inte vara alltför svårt att göra lång hand, men låt oss använda binomial sats så att när du stöter på större expansioner såsom binomials upp till 4, 5, 6, … befogenheter du vet exakt vad du ska göra.
för att komma igång måste du identifiera de två termerna från din binomial (x-och y-positionerna i vår formel ovan) och kraften (n) du utökar binomialen till.,
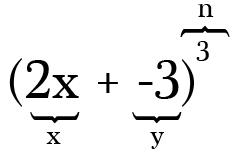
till exempel, för att expandera (2x-3)3, är de två termerna 2x och -3 och strömmen, eller n-värdet, är 3. Observera att när du har en subtraktion i din binomial är det så viktigt att komma ihåg att inkludera minus som en negativ symbol på den medföljande termen.
det underbara med binomialteoremet är att det tillåter oss att hitta det expanderade polynomet utan att multiplicera en massa binomialer tillsammans. Ganska snyggt, eller hur?, Det visar sig att antalet termer i ditt expanderade polynom alltid kommer att vara en mer än den kraft du expanderar. Det betyder att vi kommer att skapa ett polynom med 4 termer eftersom kraften i detta exempel är 3.
varje term kommer att ha en (2x) och (-3) samt ”n välj k” formel där n=3. Du kan gå vidare och skriva ner det 4 gånger, en för varje term, lämnar k-värdet i” n choose k ” och powers blank för tillfället.
nästa Vill du fylla i K-värden och befogenheter. Här kan du följa summeringsformeln, vilket ökar kraften för varje term., Men det är ganska lätt att bara följa mönstren.
k-värdena i ”n choose k” börjar med k=0 och ökar med 1 i varje term. Den sista termen ska sluta med n lika med k, i detta fall n = 3 och k=3.
nästa måste vi lägga till krafterna på (2x) och (-3).
strömmen på (2x) börjar med n-värdet, så i det här fallet 3, och kommer att minska med 1 på varje term tills du kommer till noll. Strömmen på (-3) börjar med noll och ökar med en varje gång tills du kommer till n, eller 3 i detta problem.,

eftersom något värde som höjs till nollkraften är lika med 1 kan du förenkla villkoren med nollkrafter.

fortsätt sedan och använd befogenheterna och förenkla om möjligt.,

Pascals Triangelgenväg

den sista delen är att lösa kombinationsformeln. Det uppenbara sättet att göra detta är att tillämpa kombinationsformeln för varje problem. Men vi ska ta en fin genväg med Pascals triangel.
Pascals triangel är en enkel, men kraftfull triangel som bildas genom att skapa en triangel med tre 1: or Att börja., För varje rad därefter du helt enkelt skriva 1: s i båda ändar, och hitta mittnummer(s) genom att lägga till de två värdena från direkt ovanför den.

nu är det bra. Gömd i Pascals triangel är alla svar på någon ”N välj k”! Det är som ett hemligt litet cheatsheet!
diagrammet nedan visar var den dolda ”n choose k ’s” finns.,

för vårt problem måste vi lösa för: 3 Välj 0, 3 Välj 1, 3 Välj 2 och 3 Välj 3. Vilket är alla värden i 4: e raden. Så allt vi behöver göra är att titta på den 4: e raden av Pascals triangel och matcha upp svaren.
den 4: e raden har värdena: 1, 3, 3, 1. Så jag ska bara ersätta i svaren för vår n välja k: s.,

slutligen är allt du behöver göra att multiplicera och förenkla varje term ner till sin enklaste form. Glöm inte att kontrollera ditt slutliga svar för att se till att krafterna på varje term fortfarande lägger till graden av din ursprungliga binomial! Lita på mig, det är otroligt enkelt att göra ett transkriptionsfel i den här typen av problem 😉
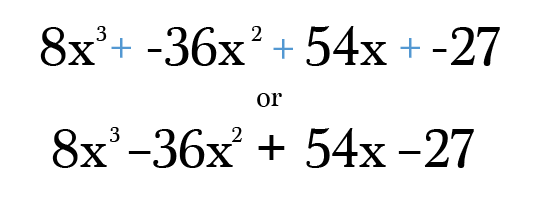
behöver du ett annat exempel?,
i videon ovan visar jag dig hur du använder Binomialteoremet för att expandera binomial (X – 3Y). Plus jag visar dig några ytterligare knep för att hålla ordning och ett par snabba kontroller som du kan använda för att enkelt identifiera vanliga fel.
Tack för att du läste!
❤ Håll kontakten ❤
Håll dig uppdaterad med allt Math Hacks är upp till!