
Dirac delta-funktionen är en funktion som introducerades 1930 av P. A. M. Dirac i hans seminal bok om kvantmekanik. En fysisk modell som visualiserar en delta-funktion är en massfördelning av ändlig total massa m-integralet över massfördelningen., När fördelningen blir mindre och mindre, medan M är konstant, krymper massfördelningen till en punktmassa, som per definition har noll utsträckning och ändå har en ändlig värderad integral lika med total massa M. i gränsen för en punktmassa blir fördelningen en Dirac delta-funktion.
heuristiskt kan Dirac delta-funktionen ses som en förlängning av Kroneckerdeltat från integrerade index (element i 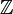 ) till verkliga index (element i
) till verkliga index (element i 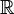 )., Observera att Kroneckerdeltat fungerar som ett ”filter” i en summering:
)., Observera att Kroneckerdeltat fungerar som ett ”filter” i en summering:
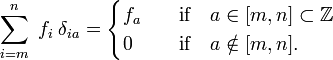
i analogi definieras Dirac−deltafunktionen δ(x-a) av (ersätt i med x och summeringen över i med en integration över x),
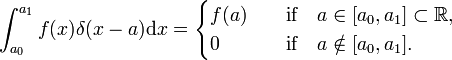
Dirac-deltafunktionen är inte en vanlig väluppfostrad karta 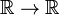 , men en distribution, även känd som en felaktig eller generaliserad funktion. Fysiker uttrycker sin speciella karaktär genom att ange att Dirac delta-funktionen bara är meningsfull som en faktor i ett integrand (”under integralen”)., Matematiker säger att deltafunktionen är en linjär funktionell på ett utrymme av testfunktioner.
, men en distribution, även känd som en felaktig eller generaliserad funktion. Fysiker uttrycker sin speciella karaktär genom att ange att Dirac delta-funktionen bara är meningsfull som en faktor i ett integrand (”under integralen”)., Matematiker säger att deltafunktionen är en linjär funktionell på ett utrymme av testfunktioner.
innehåll
- 1 Egenskaper
- 2 Delta-konvergerande sekvenser
- 2.1 Blockfunktioner
- 2.2 gaussiska funktioner
- 2.3 Lorentz-Cauchy funktioner
- 2.4 Sinc funktioner
- 3 derivat av delta-funktionen
- 3.,1 egenskaper hos derivatet
- 4 primitiva
- 5 Dirac delta-funktionen i tre dimensioner
- 6 Referenser
egenskaper
oftast tar man den nedre och den övre gränsen i definitionen av deltafunktionen lika med 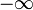 och
och 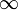 , respektive. Härifrån kommer detta att ske.
, respektive. Härifrån kommer detta att ske.
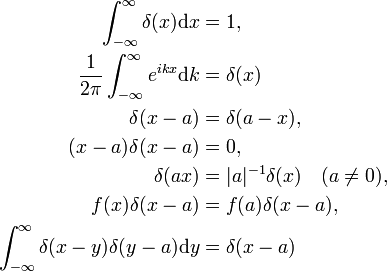
fysikens bevis på dessa egenskaper fortsätter genom att göra korrekta substitutioner i integralet och använda de vanliga reglerna för integralkalkyl., Deltafunktionen som en Fouriertransform av enhetsfunktionen f(x) = 1 (den andra egenskapen) kommer att bevisas nedan. Den sista egenskapen är analogi med multiplikationen av två identitetsmatriser,
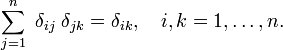
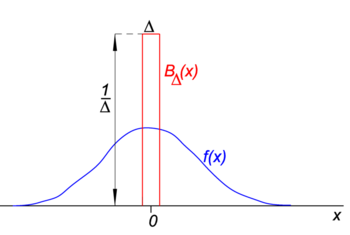
Fig. 1. Block (”boxcar”) funktion (röd) gånger reguljär funktion f(x) (Blå).
Delta-konvergerande sekvenser
det finns familjer med vanliga funktioner Fa(x) som familjemedlemmarna skiljer sig åt med värdet av en enda parameter α., Ett exempel på en sådan familj bildas av familjen gaussiska funktioner Fa (x) = exp(−ax2), där de olika värdena för den enskilda parametern α skiljer de olika medlemmarna. När alla medlemmar är linjärt normaliserbara, dvs följande integral är ändlig oavsett α,
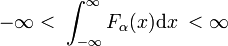
och alla medlemmar topp runt x = 0, då familjen kan bilda en delta-konvergent sekvens.,
Blockfunktioner
det enklaste exemplet på en delta-konvergent sekvens bildas av familjen av blockfunktioner, kännetecknad av positiv Δ,
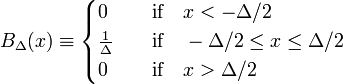
i Fig. 1 blockfunktionen BΔ visas i rött. Uppenbarligen är området (bredd gånger höjd) under den röda kurvan lika med enhet, oavsett värdet av Δ,
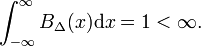
låt den godtyckliga funktionen f(x) (blå i Fig. 1) vara kontinuerlig (inga hopp) och ändlig i närheten av x=0., När Δ blir mycket liten, och blocket funktionen mycket smal(och nödvändigtvis mycket hög eftersom bredd gånger höjd är konstant) produkten f(x) BΔ(x) blir i god approximation lika med f(0) BΔ (x). Ju smalare blocket desto bättre approximation., Därför För Δ går till noll,
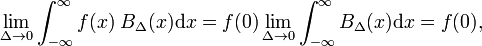
vilket kan jämföras med definitionen av deltafunktionen,
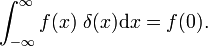
detta visar att familjen av blockfunktioner konvergerar till Dirac delta-funktionen för minskande parameter Δ; familjen bildar en delta-konvergent sekvens:
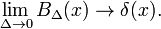
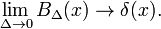
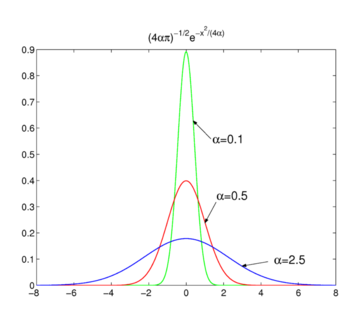
Fig. 2. Gauss funktioner.
Obs: Vi integrerade över hela den verkliga axeln., Självklart är detta inte nödvändigt, vi kunde ha uteslutit blockfunktionens nollvärderade vingar och integrerat endast över humpen i mitten, Från −Δ/2 till +Δ/2. I matematiska texter, som t.ex. Ref. , denna förfining i integrationsgränserna ingår i definitionen av deltakonvergentsekvensen. Det vill säga det krävs att integralerna över de två vingarna försvinner i gränsen. Eftersom deltakonvergerande sekvenser som uppstår i fysiska applikationer vanligtvis uppfyller detta tillstånd, utelämnar vi den mer exakta matematiska definitionen.,
gaussiska funktioner
överväga familjen,
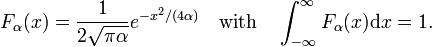
som visas i Fig. 2 funktionerna toppar runt x = 0 och blir smalare för att minska α. Därför bildar familjen gaussiska funktioner en delta-konvergent sekvens,
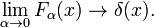
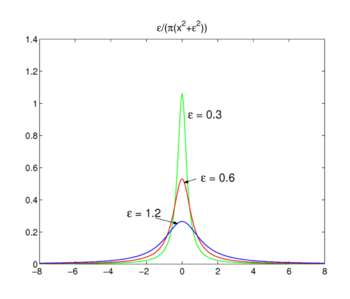
Fig. 3. Lorentz-Cauchy funktioner
Lorentz-Cauchy funktioner
familjen av funktioner som visas i Fig., 3
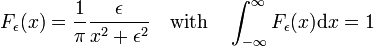
forms a delta-convergent sequence,
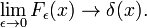
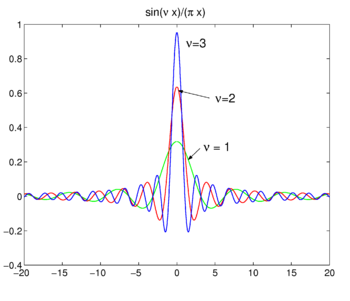
Fig. 4. Sinc functions.
Sinc functions
The family of functions (often called sinc functions) shown in Fig., 4 är
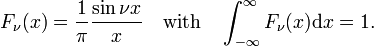
denna familj konvergerar till delta-funktionen för att öka ν
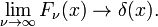
denna gräns leder lätt till Fourier integral representation av delta-funktionen:
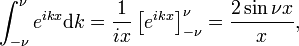
så att
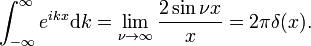
Dirac delta-funktionen är Fouriertransformen av enhetsfunktionen f(x) = 1.
derivat av deltafunktionen
överväga en differentierbar funktion f(x) som försvinner vid plus och minus oändlighet.,d=”ed7dae11d6″>
på samma sätt som man bevisar omsättningsregeln och Eremititeten hos den kvantmekaniska momentumoperatören 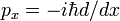 , vi visade här att d/dx är anti-Hermitisk,
, vi visade här att d/dx är anti-Hermitisk,
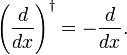
När vi skriver integralet som en inre produkt följer det av partiell integration och försvinnandet av f(x) på integrationsgränserna som vi använder.
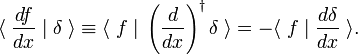
denna omsättningsregel används som definition av deltafunktionens derivat,
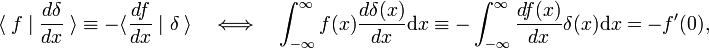
där Prime anger det första derivatet av f(x)., Enligt definitionen av deltafunktionen utvärderas det första derivatet i x = 0. Med M gånger omsättningsregeln följer att MTH −derivatet av deltafunktionen definieras av
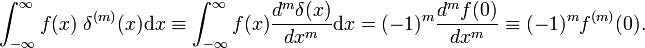
egenskaperna hos derivatet
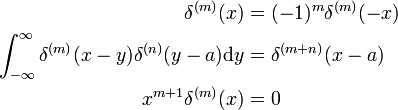
dessa resultat kan bevisas genom att substitutionen x → – x och användningen av omsättningsregeln för D/dx (se ovan) används.,
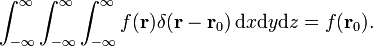
den tredimensionella deltafunktionen kan faktoriseras
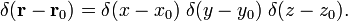
i sfäriska polära koordinater
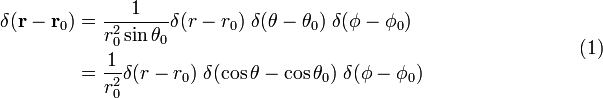
bevis på ekvation (1)
skriv
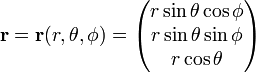
Jacobian (Jacobi determinant) av denna omvandling från kartesiska koordinater till sfäriska polära koordinater är
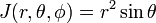
överväga
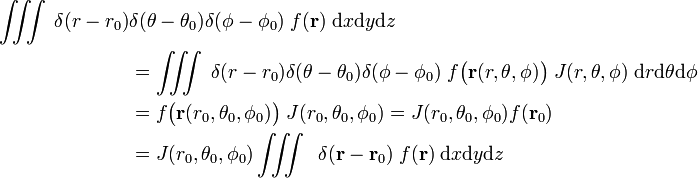
så att
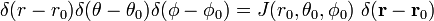
och
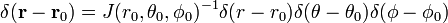
den sista raden i ekvation (1) följer av kedjeregeln.,
följande användbara och ofta tillämpade egendom bevisas här,
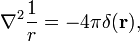
där 2 är Laplace-operatören i tredimensionella kartesiska koordinater och r är längden på r.