logaritmiska funktioner är inverser av exponentiella funktioner. Inversen av exponentiell funktion y = ax är x = ay. Den logaritmiska funktionen y = logax definieras som ekvivalent med exponentiell ekvation x = ay. y = logax endast under följande förutsättningar: x = ay, en > 0 och a≠1. Det kallas logaritmisk funktion med bas a.
Tänk på vad inversen av exponentiell funktion betyder: x = ay., Med tanke på ett nummer x och en bas a, till vilken kraft y måste en höjas till Lika x? Denna okända exponent, y, motsvarar logax. Så du ser en logaritm är inget annat än en exponent. Per definition, alogax = x, för alla reella x > 0.
nedan visas diagram i formuläret y = logax när en > 1 och när 0 < a < 1. Observera att domänen endast består av de positiva reella siffrorna, och att funktionen alltid ökar när x ökar.,
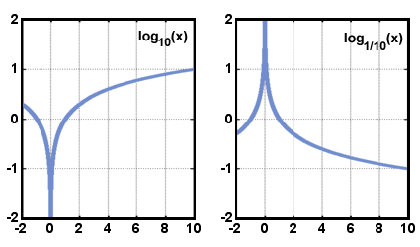
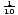 x.
x.domänen för en logaritmisk funktion är reella tal större än noll, och intervallet är reella tal. Grafen av y = logax är symmetrisk mot grafen av y = ax med avseende på linjen y = x. detta förhållande är sant för vilken funktion som helst och dess inversa.,
Here are some useful properties of logarithms, which all follow from identities involving exponents and the definition of the logarithm. Remember a > 0, and x > 0.
logarithm
| loga1 = 0. |
| logaa = 1. |
| loga(ax) = x., |
| alogax = x. |
| loga(bc) = logab + logac. |
loga(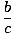 ) = logab – logac., ) = logab – logac., |
| loga(xd) = d logax |
en naturlig logaritmisk funktion är en logaritmisk funktion med bas e. f (x) = logex = ln x, där x> 0. ln x är bara en ny form av notation för logaritmer med bas e. de flesta räknare har knappar märkta ”log” och ”ln”. ”Log” – knappen förutsätter att basen är tio, och” ln ” – knappen låter naturligtvis basen lika e., Den logaritmiska funktionen med bas 10 kallas ibland den gemensamma logaritmiska funktionen. Det används i stor utsträckning eftersom vårt numreringssystem har bas tio. Naturliga logaritmer ses oftare i kalkyl.
det finns två formler som gör det möjligt att ändra basen för en logaritmisk funktion. Den första anger detta: logab = 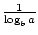 . Den mer kända och användbara formeln för att ändra baser kallas vanligtvis förändringen av basformeln. Det gör att basen för en logaritmisk funktion kan ändras till något positivt reellt nummer 1. Det står att logax =
. Den mer kända och användbara formeln för att ändra baser kallas vanligtvis förändringen av basformeln. Det gör att basen för en logaritmisk funktion kan ändras till något positivt reellt nummer 1. Det står att logax = 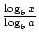 ., I det här fallet är A, B och x alla positiva reella tal och A, B, 1.
., I det här fallet är A, B och x alla positiva reella tal och A, B, 1.
i nästa avsnitt diskuterar vi några tillämpningar av exponentiella och logaritmiska funktioner.