Innehåll-konstant acceleration

innehåll

konstant acceleration

Vi är alla bekanta med det faktum att en bil snabbar upp när vi sätter vår fot ner på gaspedalen. Hastigheten för förändring av en partikels hastighet med avseende på tiden kallas dess acceleration. Om partikelns hastighet ändras med en konstant hastighet kallas denna hastighet den konstanta accelerationen.,

till exempel, om hastigheten hos en partikel som rör sig i en rak linje ändras jämnt (vid en konstant förändringshastighet) från 2 m/s till 5 m/s över en sekund, är dess konstanta acceleration 3 m/s\(^2\).

minskande hastighet

om en partikel har en initialhastighet på 6 m/s och en konstant acceleration på \(-2\) m/s\(^2\), då:

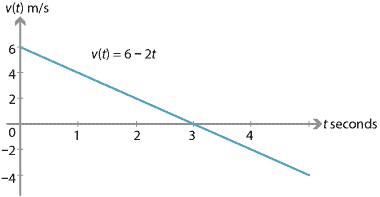
under de första tre sekunderna minskar partikelns hastighet (partikeln saktar ner). Vid tre sekunder är partikeln tillfälligt i vila., Efter tre sekunder minskar hastigheten fortfarande, men hastigheten ökar (partikeln går snabbare och snabbare).

sammanfattning

om vi antar att hastigheten för hastighetsförändring (acceleration) är en konstant, ges den konstanta accelerationen av

\

mer exakt, den konstanta accelerationen \(a\) Ges av formeln

\

där \(v(t_i)\) är hastigheten vid tiden \(t_i\). Eftersom hastigheten är en vektor, så är accelerationen.,

formlerna för konstant acceleration för rörelse i en rak linje

genom hela detta avsnitt har vi övervägt rörelse i en rak linje med konstant acceleration. Denna situation är mycket vanlig; till exempel färdas en kropp som rör sig under gravitationens påverkan med en konstant acceleration.

det antas att rörelsen börjar när \(t= 0\), och att den ursprungliga positionen tas som ursprung, det vill säga \(x(0) = 0\).,

de fem ekvationerna av rörelse

1. \(v = u + at\)
2. \(x = \dfrac{(u+v)T}{2}\)
3. \(x = ut + \dfrac{1}{2}at^2\)
4. \(V^2 = u^2 + 2AX\)
5. \(X = VT – \dfrac{1}{2}at^2\)

Obs. Var och en av de fem ekvationerna involverar fyra av de fem variablerna \(u, v, x, a, t\). Om värdena för tre av variablerna är kända kan de återstående värdena hittas genom att använda två av ekvationerna.,

härleda formlerna för konstant acceleration

den första ekvationen för rörelse

eftersom accelerationen är konstant har vi \(a = \ dfrac{v-u}{t}\). Detta ger den första ekvationen av rörelse, \(v = u + at\).

den andra ekvationen för rörelse

den andra ekvationen,

\

säger att förskjutning erhålls genom att multiplicera medelvärdet av de ursprungliga och slutliga hastigheterna med den tid som förflutit under rörelsen. Mer enkelt:

\

Vi kan härleda denna ekvation med hjälp av det faktum att förskjutningen är lika med det signerade området under hastighetstidsgrafen.,

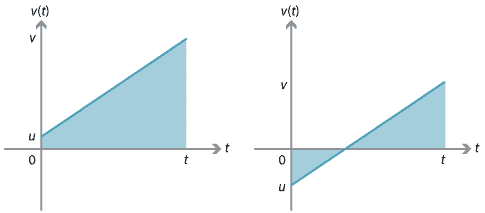
för diagrammet till höger kan förskjutningen hittas genom att överväga de två trianglarna mellan grafen och \(t\)-axeln. En av trianglarna har positivt signerat område och den andra har negativt signerat område.

att hitta förskjutningen av en partikel från hastighetsdiagrammet med integration kommer att diskuteras i ett senare avsnitt av denna modul.,

den tredje ekvationen för rörelse

som ersätter \(V\) från den första ekvationen till den andra ekvationen ger

\begin{align*}x &= \dfrac{(u+v)T}{2} \\ &= \dfrac{(u+u+at)T}{2} \\ &= \dfrac{2UT+at^2}{2} \\ &= ut + \dfrac{1}{2}at^2, \end{align*}

vilket är den tredje ekvationen. Således är \(x\) en kvadratisk i \(t\), och därmed är grafen av \(x\) mot \(t\) en parabola.

den fjärde ekvationen för rörelse

från den första ekvationen har vi \(t = \dfrac{v-u}{a}\)., Att ersätta detta i den andra ekvationen ger

\begin{align*}x &= \dfrac{(u+v)T}{2} \\ &= \dfrac{(u+v)(v-u)}{2a} \\ &= \dfrac{v^2-u^2}{2a}. \end{align*}

omarrangera för att göra\ (v^2\) motivet producerar den fjärde ekvationen:\(v^2 = u^2 + 2ax\).

den femte ekvationen för rörelse

från den första ekvationen har vi \(u = v-at\)., Med den andra ekvationen erhåller vi

\begin{align*}x &= \dfrac{(u+v)T}{2} \\ &= \dfrac{(v-at+v)T}{2} \\ &= \dfrac{2VT-at^2}{2} \\ &= vt-\dfrac{1}{2}vid^2, \end{align*}

vilket är den femte ekvationen.

vertikal rörelse

rörelse på grund av tyngdkraften är ett bra sammanhang för att demonstrera användningen av konstantaccelerationsformlerna., Som tidigare diskuterats är våra två riktningar i vertikal rörelse upp och ner, och ett beslut måste fattas om vilken av de två riktningarna som är positiv. Acceleration på grund av gravitationen är en konstant, med magnitud betecknad med \(G\). I följande exempel tar vi uppåt riktningen för att vara positiv och ta \(g= 10\) m / s\(^2\).

vidare användning av ekvationerna för rörelse

Next page – Content – Average velocity and average speed