hitta alla rötter i en polynomfunktion
använd vpasolve för att hitta alla lösningar på funktionen f(x)=6×7-2×6+3×3-8.
syms f(x)f(x) = 6*x^7-2*x^6+3*x^3-8;sol = vpasolve(f)
vpasolve returnerar sju rötter av funktionen, som förväntat, eftersom funktionen är ett polynom av grad sju.,
hitta nollor av en Nonpolynomial funktion med hjälp av sökområden och startpunkter
en plot av funktionen f (x)=e(x/7) cos(2x) avslöjar periodiska nollor, med ökande backar vid nollpunkterna när x ökar.
syms xh = fplot(exp(x/7)*cos(2*x),);grid on
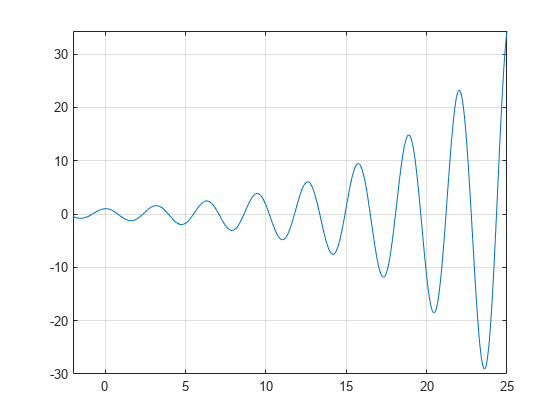
användvpasolveför att hitta en noll av funktionenf. Observera attvpasolve endast returnerar en lösning av en icke-Polynomial ekvation, även om det finns flera lösningar., On repeated calls, vpasolve returns the same result.
f = exp(x/7)*cos(2*x);for k = 1:3 vpasolve(f,x)end
ans = -7.0685834705770347865409476123789-vpa('7.0685834705770347865409476123789')
ans = -7.0685834705770347865409476123789-vpa('7.0685834705770347865409476123789')
ans = -7.0685834705770347865409476123789-vpa('7.0685834705770347865409476123789')
To find multiple solutions, set the option 'Random' to true. This makes vpasolve choose starting points randomly., For information on the algorithm that chooses random starting points, see Algorithms on the vpasolve page.
for k = 1:3 vpasolve(f,x,'Random',true)end
ans = -226.98006922186256147892598444194-vpa('226.98006922186256147892598444194')
ans = 98.174770424681038701957605727484vpa('98.174770424681038701957605727484')
ans = 52.621676947629036744249276669932vpa('52.621676947629036744249276669932')
To find a zero close to x=10, set the starting point to 10.,
vpasolve(f,x,10)
ans = 10.210176124166828025003590995658vpa('10.210176124166828025003590995658')
för att hitta noll nära x=1000, Ställ in startpunkten till1000.
vpasolve(f,x,1000)
ans = 999.8118620049516981407362567287vpa('999.8118620049516981407362567287')
för att hitta noll i intervallet 15≤x≤25, Ställ in sökintervallet till .,
vpasolve(f,x,)
ans = 21.205750411731104359622842837137vpa('21.205750411731104359622842837137')
för att hitta flera nollor i intervalletkan du inte ringavpasolve upprepade gånger eftersom det returnerar samma resultat för varje samtal, som tidigare visats. Ställ istället in sökområdet och ställ in 'Random' på true.,
for k = 1:3 vpasolve(f,x,,'Random',true)end
ans = 21.205750411731104359622842837137vpa('21.205750411731104359622842837137')
ans = 16.493361431346414501928877762217vpa('16.493361431346414501928877762217')
eftersom'Random'väljer startpunkter slumpmässigt kan samma lösning hittas vid successiva samtal.,
hitta alla nollor i ett angivet sökområde
skapa en funktionfindzeros för att systematiskt hitta alla nollor förf I ett visst sökområde, inom ett angivet feltolerans. Funktionen börjar med inmatningssökningsintervallet och anropar vpasolve för att hitta en noll. Sedan delar det sökområdet i två runt nollvärdet och kallar sig rekursivt med de nya sökområdena som ingångar för att hitta fler nollor.
funktionen förklaras avsnitt efter avsnitt här.,
deklarera funktionen med de tre ingångarna och en utgång. Den första ingången är funktionen, den andra ingången är intervallet, och den extra tredje ingången låter dig ange felet mellan en noll och de högre och nedre gränserna som genereras från den.
function sol = findzeros(f,range,err)
om du inte anger det valfria argumentet för feltolerans,findzeros angererr till0.001.
if nargin < 2 err = 1e-3;end
hitta en nolla i sökområdet medvpasolve.,
sol = vpasolve(f,range);
omvpasolve inte hittar en noll, avsluta.
if(isempty(sol)) return
omvpasolve hittar en nolla, dela upp sökområdet i två sökområden ovanför och under noll.
else lowLimit = sol-err; highLimit = sol+err;
Ringfindzeros med det lägre sökintervallet. Omfindzeros returnerar nollor kopierar du värdena i lösningsarrayen och sorterar dem.
temp = findzeros(f,,1); if ~isempty(temp) sol = sort(); end
Ringfindzeros med det högre sökområdet., Omfindzeros returnerar nollor kopierar du värdena i lösningsarrayen och sorterar dem.
temp = findzeros(f,,1); if ~isempty(temp) sol = sort(); end returnendend
hela funktionenfindzeros är som följer. Spara den här funktionen som findzeros.m I den aktuella mappen.
syms f(x)f(x) = exp(x/7)*cos(2*x);sol = findzeros(f,)'
skaffa lösningar till godtycklig Precision
använd digitsför att ställa in precisionen hos de lösningar som returneras av vpasolve., Som standard returnerarvpasolve lösningar till en precision på 32 signifikanta siffror.
f = exp(x/7)*cos(2*x);vpasolve(f)
ans = -7.0685834705770347865409476123789-vpa('7.0685834705770347865409476123789')
använddigits för att öka precisionen till 64 signifikanta siffror. När du ändrar digits, se till att du sparar det aktuella värdet så att du kan återställa det.,
digitsOld = digits;digits(64)vpasolve(f)
ans = -7.068583470577034786540947612378881489443631148593988097193625333-vpa('7.068583470577034786540947612378881489443631148593988097193625333')
nästa, ändra precisionen av lösningarna till 16 signifikanta siffror.
digits(16)
Lös multivariata ekvationer med hjälp av sökområden
överväga följande ekvationssystem.
z=10(cos(x)+cos(y))z=x+y2-0.1x2yx+y-2.7=0
en plot av ekvationerna för 0≤x≤2,5 och 0≤x≤2,5 visar att de tre ytorna skär i två punkter., För att bättre visualisera tomten, använd view. För att skala colormap-värdena, använd caxis.
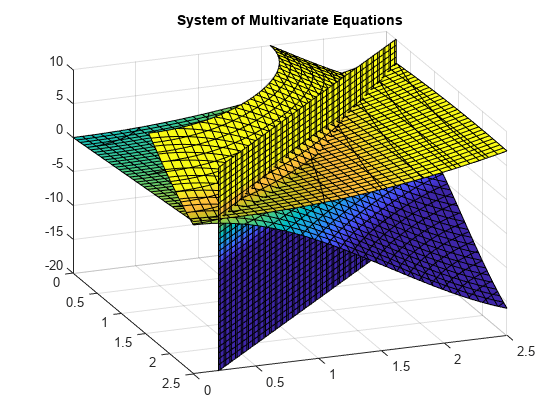
användvpasolve för att hitta en punkt där ytorna skär. Funktionenvpasolve returnerar en struktur. För att komma åtx -,y – ochz-värden för lösningen, indexera i strukturen.,
sol = vpasolve(equations);
om du vill söka efter en region i lösningsutrymmet anger du sökintervall för variablerna. Om du anger intervallen 0≤x≤1.5 och 1.5≤y≤2.5 sökervpasolve – funktionen det avgränsade området som visas.

användvpasolve för att hitta en lösning för det här sökområdet. Om du vill utelämna ett sökområde för z anger du det tredje sökområdet till .,
vars = ;range = ;sol = vpasolve(equations, vars, range);
för att hitta flera lösningar, Ställ in alternativet'Random' tilltrue. Detta gör attvpasolve använder slumpmässiga startpunkter på successiva körningar. Alternativet 'Random'kan användas tillsammans med sökområden för att göravpasolve använda slumpmässiga startpunkter inom ett sökområde. Eftersom'Random' väljer startpunkter slumpmässigt kan samma lösning hittas vid successiva samtal., Ringvpasolve upprepade gånger för att säkerställa att du hittar båda lösningarna.
Rita ekvationerna. Överlappa lösningarna som en scatter-plot med gulaX markörer med scatter3. För att bättre visualisera tomten, gör två av ytorna transparenta med alpha. Skala colormap till plotvärdena med caxisoch ändra perspektivet med view.
vpasolve hittar lösningar vid skärningspunkten mellan de ytor som bildas av ekvationerna enligt bilden.,

Lastly, restore the old value of digits for further calculations.
digits(digitsOld)