på dessa sidor tittar vi på några intressanta begrepp, vi tittar på krökt utrymme: vad krökt utrymme betyder, hur vi kan berätta om ett utrymme är krökt inifrån det eller utifrån det.
vi tittar på hur vi kan bädda in på typ av utrymme inuti en annan och se att vi kan kartlägga mellan olika utrymmen på olika sätt.
vi tittar också på compacification och hur vi kan representera oändligt stora och oändligt små vektorer i våra utrymmen på sätt som inte leder till singulariteter och andra problem.,
dessa begrepp visar sig vara användbara, även när vi arbetar med platt utrymme, hittar vi sätt att representera vektorer och plan som inte går igenom ursprunget. Detta ger oss sätt att representera rotationer och översättningar som en enda operation.
det andra programmet är relativistisk rymdtid.
Rienmannisk geometri
i rienmannisk geometri utrymme kan kurva på olika platser (se grenrör) här tittar vi på geometrier där kurvan av rymden är konstant.,
Eulideangeometri
flat space
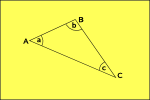
hyperbolisk geometri
rymdkurvor utåt
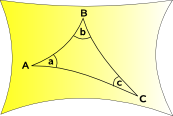
sfärisk geometri och elliptisk geometri
rymdkurvor inåt
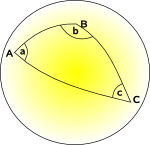
i en krökt (icke-euklidisk) geometri kan vi inte hitta en uppsättning koordinater som är ömsesidigt vinkelräta, där koordinatlinjerna alla är parallella med varandra och där varje rutnät har samma område., Vi kanske kan hitta ett koordinatsystem där vi kan göra några av dessa men inte alla.
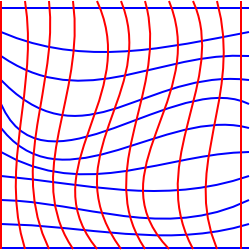
det här diagrammet försöker illustrera denna situation i 2 dimensioner, även om det är lite vilseledande, eftersom vi har ritat det på ett plan så att vi kunde ha ritat rektangulära koordinater.
för att försöka illustrera en situation där detta är omöjligt kunde vi tänka oss ett tvådimensionellt plan som har sträckts in i den tredje dimensionen.,

i den här situationen kan vi välja koordinater som bildar ett rektangulärt rutnät när de projiceras på ett horisontellt plan, dock till en person som bor i ytan då några av rutnäten verkar ha ett större område än andra och rutnätslinjerna kanske inte verkar vara parallella. Det finns inget tvådimensionellt koordinatsystem som bevarar parallella linjer, vinklar och områden samtidigt.,
ett liknande exempel försöker kartlägga jordens yta, vi kan använda latitud-och longitudlinjer men longitudlinjerna kommer närmare polerna.
i dessa fall kan vi arbeta i form av 3 dimensionella koordinater och det är ett tillvägagångssätt som vi kommer att ta med vissa typer av icke-euklidiska geometrier. Det är ofta möjligt att bädda in en viss geometri i en högre dimensionell geometri för att göra den mer euklidisk.,
det är ibland så att när vi tittar på en geometri i stor skala att den inte är euklidisk, men om vi tittar på den i mindre och mindre skala så approximerar den till en euklidisk geometri. För att göra detta måste vi hitta ett koordinatsystem där vinklar bevaras vid varje punkt, det vill säga de horisontella och vertikala koordinatlinjerna måste alltid korsas vid 90° även om linjerna kanske inte är raka. Detta är känt som en konformal geometri. I denna typ av geometri kan vi åtminstone definiera ett lokalt koordinatsystem.,
relaterat till detta är om geometrin kan differentieras och integreras, ett villkor för detta är att det måste vara välskött och inte ha några plötsliga hopp etc. Vissa geometrier och koordinatsystem kan vara väluppfostrade på vissa ställen men har singulariteter etc.
för diskussion om hur krökningen mäts, se den här sidan.
matematisk Notation
hur hanterar vi geometrier där vi inte kan använda alla regler som gäller för euklidisk geometri?,
ett tillvägagångssätt är att använda tensor notation, detta ger konventioner och notation som hjälper oss att byta mellan olika koordinatsystem. Ett ortogonalt koordinatsystem, lokalt till vilken punkt som helst, kan definieras med hjälp av basvektorer som är tangenter till koordinatlinjerna.,Manifold
se den här sidan
förhållandet mellan hyperbolisk och Minkowski geometrier
| Minkowski geometri | hyperbolisk geometri | |
| punkt | händelse i rymdtid | partikel i enhetlig rörelse |
| avstånd mellan två punkter | tidsintervall mellan två händelser | relativ hastighet mellan två sådana partiklar |
terminologi
här tittar vi på terminologin som geometrier, utrymmen, modeller, prognoser och transformationer., Dess ganska svårt när vi börjar hantera icke-euklidiska geometrier eftersom vi använder liknande terminologi som vi är vana vid i konventionella euklidiska utrymme men termerna kan ha något olika egenskaper.,prova
elliptisk geometri
modeller
exempel är:
- övre halvplansmodell
- Poincare disc Modell
- projektiv Modell
- konformell modell
projektioner
stereografisk projektion
förvandlar
invariant
exempel är:
- Möbius transform
- Lorentz transform
parallell postulat
om vi tar bort det parallella postulatet från euklidiskt utrymme.,
detta leder till:
- parallell postulat är falskt
- vinklarna i en triangel lägger inte till π
- för en form av en viss storlek finns det inte i allmänhet en liknande form av en större storlek.,ctive
conformal (Poincaré disc ) raka linjer – geodesics segment av cirklar vinkel bevara mer interna vinklar av triangeln π-(α+β+γ)=cδ avstånd mellan två punkter med