ändliga automater kan ha utgångar som motsvarar varje övergång. Det finns två typer av ändliga tillstånd maskiner som genererar utgång-
- mjölig maskin
- Moore maskin
mjölig maskin
en mjölig maskin är en FSM vars utgång beror på nuvarande tillstånd samt nuvarande ingång.,
det kan beskrivas med en 6 tuple (Q, Trip, O, δ, X, q0) där −
-
Q är en ändlig uppsättning stater.
-
är en ändlig uppsättning symboler som kallas inmatningsalfabet.
-
O är en ändlig uppsättning symboler som kallas utdata alfabet.
-
δ är ingångsövergångsfunktionen där δ: q × → Q
-
X är utgångsövergångsfunktionen där X: Q × → o
-
q0 är det ursprungliga tillståndet från vilket någon ingång bearbetas ( q0 Q).,b424468″>
Output
The state diagram of the above Mealy Machine is −
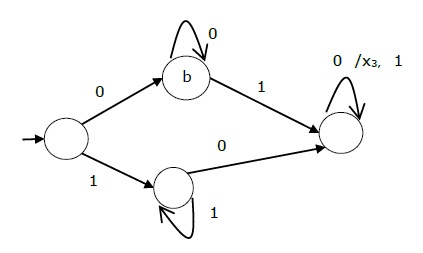
Moore Machine
Moore machine is an FSM whose outputs depend on only the present state.,
en Moore-maskin kan beskrivas med en 6 tuple (Q, Trip, O, δ, X, q0) där −
-
Q är en ändlig uppsättning stater.
-
är en ändlig uppsättning symboler som kallas inmatningsalfabet.
-
O är en ändlig uppsättning symboler som kallas utdata alfabet.
-
δ är inmatningsövergångsfunktionen där δ: q × → Q
-
X är utmatningsövergångsfunktionen där X: q → o
-
q0 är det ursprungliga tillståndet från vilket någon ingång bearbetas (q0 must Q).,iv>
Present state Next State Output Input = 0 Input = 1 → a b c x2 b b d x1 c c d x2 d d d x3 The state diagram of the above Moore Machine is −
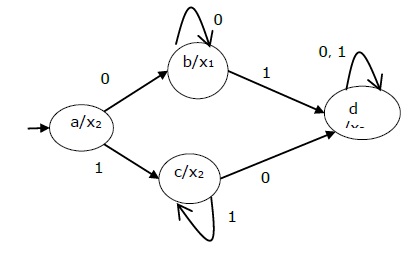
Mealy Machine vs., Moore Machine
Följande tabell belyser de punkter som skiljer en mjölkmaskin från en Moore-maskin.
mjölig maskin Moore maskin utdata beror både på nuvarande tillstånd och nuvarande ingång utdata beror endast på nuvarande tillstånd. generellt har det färre tillstånd än Moore-maskinen. generellt har det fler stater än mjölkmaskin., värdet på utmatningsfunktionen är en funktion av övergångarna och ändringarna, när inmatningslogiken i nuvarande tillstånd är klar. värdet på utmatningsfunktionen är en funktion av det aktuella tillståndet och ändringarna vid klockkanterna, när tillståndsändringar inträffar. mjöliga maskiner reagerar snabbare på ingångar. De reagerar i allmänhet i samma klockcykel. i Moore-maskiner krävs mer logik för att avkoda utgångarna vilket resulterar i fler kretsfördröjningar. De reagerar i allmänhet en klockcykel senare., Moore Machine to Mealy Machine
algoritm 4
Input − Moore Machine
Output − Mealy Machine
Steg 1 − Ta en tom Mealy Machine transition table format.
steg 2 − kopiera alla Moore-maskinens övergångstillstånd till det här tabellformatet.
steg 3-Kontrollera nuvarande tillstånd och deras motsvarande utgångar i Moore-maskinstabellen; om Qi-utmatningen är m, kopiera den till utdatakolumnerna i Mealy-maskinstabellen där Qi visas i nästa tillstånd.,der the following Moore machine −
Present State Next State Output a = 0 a = 1 → a d b 1 b a d 0 c c c 0 d b a 1 Now we apply Algorithm 4 to convert it to Mealy Machine.,8″>
Output
Mealy Machine to Moore Machine
Algorithm 5
Input − Mealy Machine
Output − Moore Machine
Step 1 − Calculate the number of different outputs for each state (Qi) that are available in the state table of the Mealy machine.,
steg 2 − om alla utgångar för Qi är desamma, kopiera tillstånd Qi. Om det har n distinkta utgångar, bryta Qi i n stater som Qin där n = 0, 1, 2…….
steg 3-om utmatningen från det ursprungliga tillståndet är 1, Sätt in ett nytt initialtillstånd i början som ger 0-utmatning.,b424468″>
Output
Here, states ‘a’ and ‘d’ give only 1 and 0 outputs respectively, so we retain states ‘a’ and ‘d’., Men staterna ” b ” och ” c ” producerar olika resultat (1 och 0). Så delar vi b i B0, b1 och C i C0, c1.,”>
Output