en nollhypotes är ett exakt uttalande om en population som vi försöker avvisa med provdata.Vi brukar inte tro att vår nollhypotes (eller H0) är sann. Vi behöver dock ett exakt uttalande som utgångspunkt för statistisk signifikanstestning.
Nollhypotesexempel
ofta-men inte alltid – anger nollhypotesen att det inte finns någon koppling eller skillnad mellan variabler eller subpopulationer., Liksom så är några typiska null-hypoteser:
- korrelationen mellan frustration och aggression noll (korrelationsanalys);
- Den genomsnittliga inkomsten för män liknar den för kvinnor (oberoende prover t-test);
- nationalitet är (perfekt) orelaterad med musikpreferens (chi-square independence test);
- Den genomsnittliga befolkningsinkomsten var lika med 2012 till 2016 (upprepade åtgärder ANOVA).
”Null” betyder inte ”noll”
ett vanligt missförstånd är att ”null” innebär ”noll”. Detta är ofta men inte alltid fallet., Till exempel kan en nollhypotes också ange attkorrelationen mellan frustration och aggresion är 0.5.No noll inblandade här och – även om något ovanligt-helt giltigt.
”null ” i” nollhypotesen ”härrör från”nollställa” 5: nollhypotesen är uttalandet att vi försöker motbevisa, oavsett om det gör (inte) anger en noll effekt.
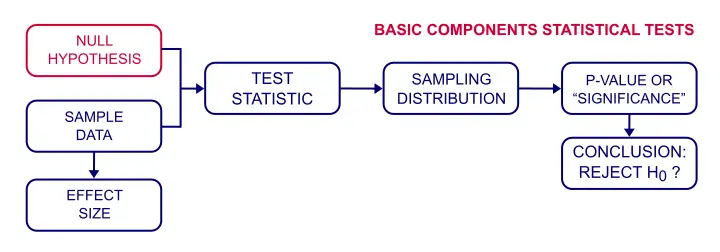
Nollhypotestestning-Hur fungerar det?
Jag vill veta om lycka är relaterad till rikedom bland Nederländska människor. Ett sätt att ta reda på detta är att formulera en nollhypotes., Eftersom ”relaterat till” inte är exakt väljer vi motsatt uttalande som vår nollhypotes:korrelationen mellan rikedom och lycka är noll bland alla nederländska människor.Vi ska nu försöka motbevisa denna hypotes för att visa att lycka och rikedom är relaterade okej.
Nu kan vi inte rimligen fråga alla 17,142,066 holländska människor hur glada de i allmänhet känner.

Så vi frågar ett prov (säg 100 personer) om deras rikedom och deras lycka. Korrelationen mellan lycka och rikedom visar sig vara 0,25 i vårt prov., Nu har vi ett problem: provresultat tenderar att skilja sig något från befolkningens resultat. Så om korrelationen verkligen är noll i vår befolkning, kan vi hitta en icke noll korrelation i vårt prov. För att illustrera denna viktiga punkt, ta en titt på scatterplot nedan. Det visualiserar en noll korrelation mellan lycka och rikedom för en hel befolkning på n = 200.

nu ritar vi ett slumpmässigt urval av N = 20 från denna population (de röda prickarna i vår tidigare scatterplot). Även om vår befolkningskorrelation är noll, hittade vi en svindlande 0.,82 korrelation i vårt prov. Figuren nedan illustrerar detta genom att utelämna alla icke samplade enheter från vår tidigare scatterplot.

detta väcker frågan hur vi någonsin kan säga något om vår befolkning om vi bara har ett litet prov från det. Det grundläggande svaret: Vi kan sällan säga något med 100% säkerhet. Men vi kan säga mycket med 99%, 95% eller 90% säkerhet.
Sannolikhet
Så hur fungerar det? I grund och botten är vissa provresultat högst osannolika med tanke på vår nollhypotes., Som så visar figuren nedan sannolikheterna för olika provkorrelationer (N = 100) om populationskorrelationen verkligen är noll.

en dator kommer lätt att beräkna dessa sannolikheter. Detta kräver dock en provstorlek (100 i vårt fall) och en förmodad befolkningskorrelation ρ (0 i vårt fall). Därför behöver vi en nollhypotes.
om vi tittar på denna provtagningsfördelning noggrant ser vi att provkorrelationer runt 0 är mest troliga: det finns en 0.68 sannolikhet att hitta en korrelation mellan -0.1 och 0.1. Vad betyder det?, Kom ihåg att sannolikheter kan ses som relativa frekvenser. Så tänk dig att vi skulle rita 1000 prover istället för den vi har. Detta skulle resultera i 1,000 korrelationskoefficienter och några 680 av dem-en relativ frekvens på 0,68 – skulle ligga i intervallet -0.1 till 0.1. På samma sätt finns det en 0.95 (eller 95%) sannolikhet att hitta en provkorrelation mellan -0.2 och 0.2.
p-värden
Vi hittade en provkorrelation på 0,25. Hur sannolikt är det om befolkningskorrelationen är noll?, Svaret är känt som p-värdet (kort för sannolikhetsvärde):ett p-värde är sannolikheten att hitta något provresultat eller en mer extrem om nollhypotesen är sann.Med tanke på vår 0.25 korrelation betyder ”mer extrem” vanligtvis större än 0.25 eller mindre än -0.25. Vi kan inte se från vår graf men den underliggande tabellen berättar att p 0.012. Om nollhypotesen är sann finns det en 1.2% sannolikhet att hitta vår provkorrelation.
slutsats?
om vår befolkningskorrelation verkligen är noll kan vi hitta en provkorrelation på 0,25 i ett prov på N = 100., Sannolikheten för att detta händer är bara 0,012 så det är väldigt osannolikt. En rimlig slutsats är att vår befolkningskorrelation inte var noll trots allt.
slutsats: vi avvisar nollhypotesen. Med tanke på vårt provresultat tror vi inte längre att lycka och rikedom är orelaterade. Men vi kan fortfarande inte säga detta med säkerhet.
nollhypotes – begränsningar
hittills har vi bara dragit slutsatsen att befolkningskorrelationen förmodligen inte är noll. Det är den enda slutsatsen från vår nollhypotes tillvägagångssätt och det är inte riktigt så intressant.,
vad vi verkligen vill veta är befolkningskorrelationen. Vår provkorrelation på 0,25 verkar vara en rimlig uppskattning. Vi kallar ett sådant enda nummer en punktskattning.
Nu kan ett nytt prov komma med en annan korrelation. En intressant fråga är hur mycket våra prov korrelationer skulle fluktuera över prover om vi skulle dra många av dem. Figuren nedan visar exakt det, förutsatt att vår provstorlek på n = 100 och vår (punkt) uppskattning av 0.25 för befolkningskorrelationen.,

konfidensintervall
vårt provresultat tyder på att cirka 95% av många prover skulle komma med en korrelation mellan 0,06 och 0,43. Detta intervall är känt som ett konfidensintervall. Även om det inte är exakt korrekt är det lättast om det är bandbredden som sannolikt kommer att omsluta befolkningskorrelationen.
en sak att notera är att concidensintervallet är ganska brett. Det innehåller nästan en nollkorrelation, exakt nollhypotesen vi avvisade tidigare.,
en annan sak att notera är att vårt urvalsfördelning och konfidensintervall är något asymmetriska. De är symmetriska för de flesta andra statistik (t.ex. medel eller beta-koefficienter) men inte korrelationer.