
har du någonsin undrat hur kan det snöa vid över frystemperaturer? Tja, den naiva förklaringen är att det helt enkelt tar tid för snöflingorna att smälta när de tränger in över frysluften, eftersom de faller nedåt till marken. Detta är naturligtvis anledningen till att hagel kan falla i varmt väder. Helt enkelt hagel stenar faller snabbt, för snabbt att låta den varma luften smälta hagel. Detta är inte den viktigaste förklaringen, men för varför det kan snö när det är över frysning.,
från figuren nedan är det uppenbart att det finns ett tydligt beroende av luftfuktigheten – ju torrare det är desto varmare kan det vara medan det snöar. Detta innebär att huvudfaktorn, åtminstone under torra förhållanden, har att göra med fuktighet. Och denna faktor är avdunstning. Mer specifikt, när snöflingorna faller, avdunstar de. Denna process tar värme och håller flingorna kalla.
således, om vi vill beräkna den maximala temperaturen, måste vi uppskatta netto värmebalansen i flingan. Först, när flingorna reser i en varm miljö, får de värme från omgivningen genom ledning., För det andra används värme för att förånga flingorna och därigenom kyla dem. Om förångningsvärmen ”sink” är större än värmeledningen, kommer flingorna att förbli frysta.
det visar sig att detta lätt kan beräknas. Nej, det är inte enkelt att beräkna värmeledningen eller förångningsvärmen, men förhållandet är, eftersom olika okända geometriska faktorer avbryter.
om du inte bryr dig om beräkningen (eftersom du inte är en science freak), kan du helt enkelt besöka räknaren sidan.
om du bryr dig, här är härledningen., Antag att flödet runt flingorna är sådant att ett gränsskikt av bredd d bildas runt det. Det totala värmeflödet $f_h$ till flingan (t.ex. J/SEK i MKs) kommer att ges av Fouriers lag:
där $\kappa$ är värmediffusionskoefficienten för luft (t. ex. m2/SEK i MKs), C är luftvärmekapaciteten (J/kg i MKS), A är gränsskiktets yta runt flingan, medan det totala värmeflödet $ f_h $ till flingan (t. ex. δt är temperaturskillnaden mellan flingan och miljön.,
på samma sätt kan man använda ficks lag för att erhålla diffusion av vattenånga från flingan (där temperaturen är nära frysning och den relativa luftfuktigheten är 100%), till omgivningen, där temperaturen är högre och den relativa luftfuktigheten lägre:
här är d vattendiffusionskoefficienten (t.ex. m2/SEK i MKS) och ρ är vattenångdensiteten (kg/m3 i MKS).,
Den förångande isen kräver värme, så om det finns ett vattenånga massflöde av Φ Från flingan, skulle det kräva värme med en hastighet av $f_w = \ epsilon \ Phi$ där $ \ epsilon$ är värmen av förångning av is (J/kg i MKS).
Den högsta temperaturen över vilken snöflingan smälter är den temperatur för vilken de två värmeflödena är lika:
Observera att geometrin för flödet runt flingan avbryts, eftersom båda värmeflödena beror på D och A på samma sätt., Detta skulle vara fallet även om gränsskiktet runt flingan är komplext så att d faktiskt beror på riktningen. Därför
där$ \rho_{sat} $ är mättnadens vattenånga densitet.
pluggning i siffrorna (som kan hittas till exempel i CRC handbook of chemistry and physics), resulterar med en implicit ekvation för temperatureneftersom mättnadstätheten för vattenånga beror också på temperaturen., Vi kan förenkla saker om vi istället frågar Vad är den relativa luftfuktigheten som krävs för att hålla flingan frusen vid en viss temperatur. Det är:
där$ T_C $ är temperaturen i grad Celsius.
Denna funktion kan ses i figuren nedan, tillsammans med data från Matsuo och Sasyo, 1981. Som framgår av figuren är den beräknade grafen ungefär den nedre gränsen under vilken det inte finns något regn alls. Vid varmare temperaturer finns en blandning., Upp till ca 1 ° C över ingen smältlinje, det finns mestadels snö medan mellan ca 1 ° C och 2 ° C över linjen, det är mestadels regn, men snö är möjligt. Dessa händelser kan bero på ytterligare effekter, såsom starka neddragningar, tid det tar att smälta snön etc.
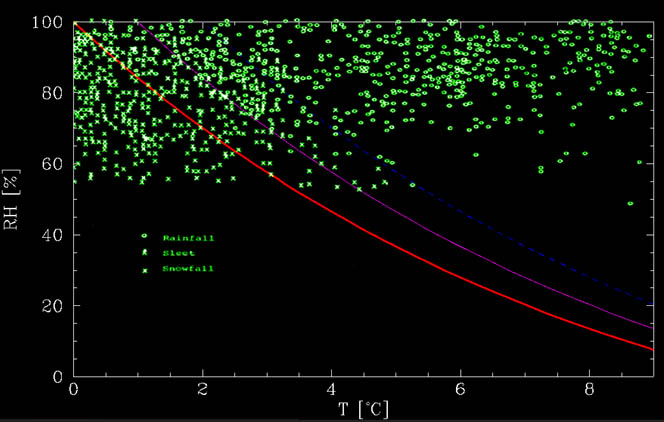
om vi vill observera varmt väder snö krävs därför mycket torra förhållanden. Till exempel, om markfuktigheten är endast ca 20% (mycket sällsynt, för om det finns Nederbörd, är atmosfären i allmänhet våt!) då kan det snöa vid 8 ° C (eller 46°F för engelska användare).,
ett annat krav är att ingenstans längs nedstigningen överträffar luften ingen smältlinje. Om det gör det, smälter flingan naturligtvis.
om temperaturen stiger över frysning finns det inga parametrar med vilka typen av nederbörd kan bestämmas för säkerhet. Allt som vi sedan kan förutsäga är sannolikheten att snön faktiskt kommer att falla. Detta kan göras med hjälp av resultaten från häggmark och Ivarsson (1997), endast korrigerad för att använda den frusna glödlampan och inte våtlampans temperatur.
Den nedersta raden är en kalkylator med vilken sannolikheten för snö kan uppskattas.,