egenskaper för områden
Centroid
Centroid av en form representerar den punkt om vilken sektionsområdet är jämnt fördelat. Om området är dubbelt symmetriskt om två ortogonala axlar ligger centroiden vid skärningspunkten mellan dessa axlar. Om området är symmetriskt om endast en axel ligger centroiden någonstans längs den axeln (den andra koordinaten måste beräknas)., Om den exakta platsen för centroiden inte kan bestämmas genom inspektion kan den beräknas med:
|
|
|
där da representerar området för ett oändligt litet element, A är tvärsnittets totala yta, och X och Y är koordinaterna för element da med avseende på intresseaxeln.,
centroidalplatserna för vanliga tvärsnitt är väl dokumenterade, så det är vanligtvis inte nödvändigt att beräkna platsen med ekvationerna ovan., av grundläggande former vars centroidala platser är kända med avseende på någon referenspunkt, kan den centroidala platsen för det sammansatta tvärsnittet beräknas som:
|
|
|
där XC,i och YC är jag de rektangulära koordinaterna för den centroidala platsen för ith-sektionen med avseende på referenspunkten,och AI är området för ith-sektionen.,
Centroidala avståndet
centroidala avståndet, c, är avståndet från centroid av ett tvärsnitt till den extrema fibern., Det centroidala avståndet I Y-riktningen för ett rektangulärt tvärsnitt visas i figuren nedan:
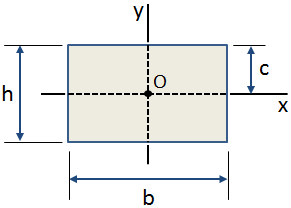
vanliga användningsområden för centroidala avstånd inkluderar:
- beräkning av den maximala böjspänningen i ett tvärsnitt
- beräkning av värdet för det första ögonblicket av området, Q, ovanför en punkt i tvärsnittet för att bestämma skjuvningen.stress vid den punkten
Vi har ett antal strukturella räknare att välja mellan.,
- Beam Calculator
- Bolted joint Calculator
- Bolt Pattern Force Distribution
- Lug Calculator
- kolumn Buckling Calculator
- trötthet Crack Growth Calculator

första ögonblicket av området
det första ögonblicket i ett område med avseende på en intresseaxel beräknas som:
| QX = y da | QY = X da |
där QX är det första ögonblicket om x-axeln och QY är det första ögonblicket om Y-axeln.,Om området består av en samling av grundläggande former vars centroidala platser är kända med avseende på intresseaxeln, kan det första ögonblicket i kompositytan beräknas som:
|
|
|
|
Observera att det första ögonblicket av området används vid beräkning av centroiden av ett tvärsnitt med avseende på något ursprung (som diskuterats tidigare)., Det första ögonblicket används också vid beräkning av värdet av skjuvspänning vid en viss punkt i tvärsnittet. I detta fall beräknas det första ögonblicket för ett område som utgör en mindre del av tvärsnittet, där området begränsas av intressepunkten och tvärsnittets extrema fiber (topp eller botten). Det första ögonblicket beräknas om en axel som passerar genom tvärsnittets centroid.,
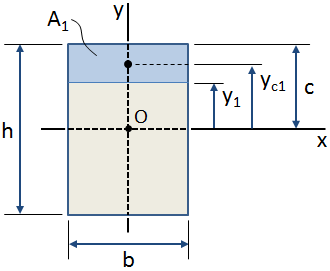
i figuren ovan är det skuggade blå området intresseområdet inom det övergripande tvärsnittet.,X-axeln (som passerar genom tvärsnittet centroid, punkt O i figuren ovan) beräknas som:
om den centroidala platsen för intresseområdet är känd, kan det första ögonblicket av området med avseende på axeln beräknas som (se figuren nedan). ovan):
det bör noteras att det första ögonblicket av ett område kommer att vara positivt eller negativt beroende på positionen för området med avseende på ränteaxeln., Därför kommer det första ögonblicket av hela området av ett tvärsnitt med avseende på sin egen centroid att vara noll.
tröghetsmoment
det andra ögonblicket av området, mer allmänt känt som tröghetsmomentet, I, av ett tvärsnitt är en indikation på en strukturell medlems förmåga att motstå böjning.,(Not 1) Ix och Iy är tröghetsmomenten om x – respektive y – axlarna och beräknas med:
| Ix = Y2 da | IY = x2 da |
där x och y är koordinaterna för element dA med avseende på axeln av intresse.
oftast beräknas tröghetsmomenten med avseende på sektionens centroid. I detta fall kallas de centroidala tröghetsmoment och betecknas som Icx för trögheten om X-axeln och Icy för trögheten om y-axeln.,
tröghetsmomenten för vanliga tvärsnitt är väl dokumenterade, så det är vanligtvis inte nödvändigt att beräkna dem med ekvationerna ovan. Egenskaper för flera vanliga tvärsnitt ges i slutet av denna sida.
om ett tvärsnitt består av en samling av grundläggande former vars centroider alla sammanfaller, är tröghetsmomentet i den sammansatta sektionen helt enkelt summan av de enskilda ögonblicken av tröghet. Ett exempel på detta är en boxstråle som består av två rektangulära sektioner, som visas nedan., I detta fall har den yttre sektionen ” positivt område ”och den inre sektionen har” negativt område”, så det sammansatta tröghetsmomentet är subtraktionen av tröghetsmomentet i den inre sektionen från den yttre sektionen.
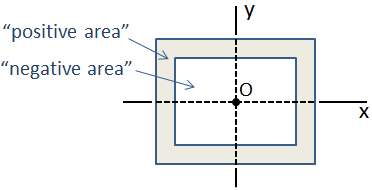
Vid ett mer komplicerat sammansatt tvärsnitt där centroidalplatserna inte sammanfaller kan tröghetsmomentet beräknas med parallellaxelns teorem.
det är viktigt att inte förväxla tröghetsmomentet i ett område med tröghetsmomentet i en fast kropp., Tröghetsmomentet indikerar ett tvärsnitt motstånd mot böjning, medan tröghetsmomentet indikerar kroppens motståndskraft mot rotation.,
parallell axel Sats
om tröghetsmomentet för ett tvärsnitt om en centroidal axel är känt, kan parallell axelsatsen användas för att beräkna tröghetsmomentet om någon parallell axel:
där Ic är tröghetsmomentet om centroidalaxeln, d är det värde som används för att beräkna tröghetsmomentet.avståndet mellan den centroidala axeln och den parallella axeln, och A är tvärsnittets område.,
om ett tvärsnitt består av en samling av grundläggande former vars centroidala tröghetsmoment är kända tillsammans med centroidernas avstånd till någon referenspunkt, kan parallellaxelns teorem användas för att beräkna tröghetsmoment i det sammansatta tvärsnittet.
till exempel kan en I-stråle approximeras med 3 rektanglar, som visas nedan. Eftersom denna kompositsektion är symmetrisk om både x – och y-axlarna, kan snittets centroid placeras genom inspektion vid skärningspunkten mellan dessa axlar. Centroiden ligger vid ursprunget, O, i figuren.,
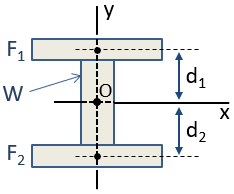
tröghetsmomentet i kompositsektionen kan beräknas med hjälp av parallellaxelns sats. Sektionens centroidala tröghetsmoment om x-axeln, Icx, beräknas som:
där Icx-termerna är tröghetsmomenten för de enskilda sektionerna om sina egna centroider i X-axelns orientering, är d-termerna avstånden för de enskilda sektionscentroiderna till kompositsektionen centroid och A-termerna är områdena för de enskilda sektionerna. Eftersom Centroid av sektion W och centroid av den sammansatta sektionen är sammanfallna, är d noll för den sektionen och så finns det ingen Ad2-term.,
det är viktigt att notera konsekvenserna av parallellaxelns teorem att som en enskild sektion rör sig längre från centroiden av kompositsektionen, ökar bidraget från den sektionen till kompositsektionens tröghetsmoment med en faktor d2. Därför, om avsikten är att öka tröghetsmomentet i en sektion om en viss axel, är det mest effektivt att lokalisera området så långt från den axeln som möjligt. Detta förklarar formen på en I-stråle., Flänsarna är de främsta bidragsgivarna till tröghetsmomentet, och webben tjänar till att skilja flänsarna från böjningsaxeln. Banan behöver dock behålla viss tjocklek för att undvika buckling och eftersom webben tar en betydande del av skjuvspänningen i avsnittet.
polärt tröghetsmoment
tröghetens polära ögonblick, i, av ett tvärsnitt är en indikation på en strukturell medlems förmåga att motstå vridning om en axel vinkelrätt mot sektionen., Polarmomentet av tröghet för en sektion med avseende på en axel kan beräknas med:
där x och y är koordinaterna för element dA med avseende på axeln av intresse, och r är avståndet mellan elementet dA och axeln av intresse.,
även om det polära tröghetsmomentet kan beräknas med hjälp av ekvationen ovan, är det vanligtvis bekvämare att beräkna det med hjälp av den vinkelräta axelns teorem, som anger att det polära tröghetsmomentet i ett område är summan av tröghetsmomenten om två ortogonala axlar som passerar genom intresseaxeln:
oftast passerar intresseaxeln genom axeln.tvärsnittets centroid.,
Sektionsmodulen
den maximala böjspänningen i en stråle beräknas som σb = Mc / Ic, där C är avståndet från den neutrala axeln till den extrema fibern, Icis tröghetscentroidmomentet och M är böjmomentet. Sektionsmodulen kombinerar C-och Ic-termerna i böjspänningsekvationen:
med hjälp av sektionsmodulen beräknas böjspänningen som σb = M / S. användbarheten av sektionsmodulen är att den karakteriserar böjmotståndet hos ett tvärsnitt på en enda term., Detta möjliggör optimering av en stråls tvärsnitt för att motstå böjning genom att maximera en enda parameter.
Gyrationsradie
gyrationsradien representerar avståndet från en sektionens centroid där hela området kan koncentreras utan att ha någon effekt på tröghetsmomentet.,>
A polar radius of gyration can also be calculated for problems involving torsion about a centroidal axis:
The rectangular radii of gyration can also be used to calculate the polar radius of gyration:
We have a number of structural calculators to choose from., Här är bara några:
- Beam Calculator
- Bolted joint Calculator
- Bolt Pattern Force Distribution
- Lug Calculator
- kolumn Buckling Calculator
- trötthet Crack Growth Calculator

egenskaper hos gemensamma tvärsnitt
tabellen nedan ger egenskaper för gemensamma tvärsnitt. Mer omfattande tabeller finns i de listade referenserna.
de egenskaper som beräknas i tabellen inkluderar area, centroidal moment av tröghet, avsnitt modul, och radie av gyration.,
Vi har ett antal strukturella räknare att välja mellan., Här är bara några:
- Beam Calculator
- Bolted joint Calculator
- Bolt Pattern Force Distribution
- Lug Calculator
- kolumn Buckling Calculator
- trötthet spricka tillväxt kalkylator

anteckningar
anmärkning 1: avböjning av en stråle
avböjningen av en stråle under böjning bestäms av tröghetsmomentet i tvärsnittet, strålens längd och materialets elastiska modul. Mer detaljer ges i denna diskussion om balkavböjning.