” Unit Circle ” är en cirkel med en radie på 1.
det är så enkelt, det är ett bra sätt att lära sig och prata om längder och vinklar.
centret sätts på ett diagram där x-axeln och y-axeln korsar, så vi får det här snygga arrangemanget här.
sinus, cosinus och Tangent
eftersom radien är 1 kan vi direkt mäta sinus, cosinus och tangent.,
vad händer när vinkeln, θ, är 0°?
cos 0° = 1, sin 0° = 0 och tan 0° = 0
vad händer när θ är 90°?
cos 90° = 0, sin 90° = 1 och tan 90 ° är odefinierad
prova själv!
försök!, Flytta musen runt för att se hur olika vinklar (i radianer eller grader) påverkar sinus, cosinus och tangent
”sidorna” kan vara positiva eller negativa enligt reglerna för kartesiska koordinater. Detta gör sinus, cosinus och tangent förändring mellan positiva och negativa värden också.
prova också den interaktiva enhetscirkeln.,
Pythagoras
Pythagoras sats säger att för en rätvinklig triangel är kvadraten på långsidan lika med summan av kvadraterna på de andra två sidorna:
x2 + y2 = 12
men 12 är bara 1, Så:
x2 + y2 = 1
(ekvationen för enhetscirkeln)
också, eftersom x=cos och y=sin får vi:
(cos(θ))2 + (Sin(θ))2 = 1
en användbar ”identitet”
viktiga vinklar: 30°, 45° och 60°
Du bör försöka att komma ihåg synd, cos och solbränna för vinklarna 30°, 45° och 60°.,
Ja, ja, det är en smärta att komma ihåg saker, men det kommer att göra livet enklare när du känner dem, inte bara i tentor, men andra gånger när du behöver göra snabba uppskattningar etc.
det här är de värden du bör komma ihåg!,id=”0f47f3223b”>
What about tan?,
Tja, tan = sin / cos, så vi kan beräkna det så här:
tan(30°) =sin (30°)cos(30°) = 1/2√3/2 = 1√3 = √33 *
tan (45°) = sin(45°) cos(45°) = √2/2√2/2 = 1
tan(60°) =sin (60°)cos(60°) = √3/21/2 = √3
* Obs: skriva 1√3 kan kosta dig märken (se rationella nämnare), så istället använda √33
snabb skiss
ett annat sätt att hjälpa dig att komma ihåg 30° och 60° är att göra en snabb skiss:
| rita en triangel med sidlängder på 2 | 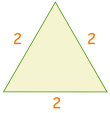 |
|
|
halveras.,div id=”56c966b492″> exempel: sin(30°)sinus: sohcahtoa sinus är motsatt dividerat med hypotenusan
sin(30°) = oppositehypotenuse = 12
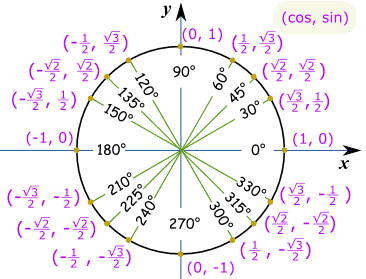
hela cirkelnför hela cirkeln behöver vi värden i varje kvadrant, med rätt plus-eller minustecken enligt kartesiska koordinater: Observera att Cos är först och synden är andra, så det går (cos, sin):
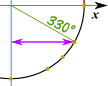
spara som PDF exempel: vad är cos(330°) ?,
gör en skiss så här, och vi kan se att det är det ”långa” värdet: √32 och det här är samma enhetscirkel i radianer.
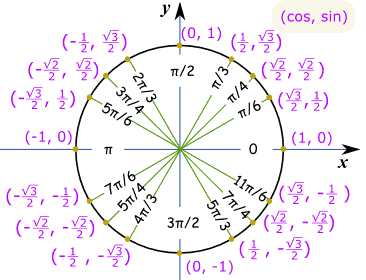
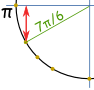
exempel: Vad är synd(7π / 6) ?
Tänk ”7π/6 = π + π/6” och gör sedan en skiss. vi kan sedan se att det är negativt och är ”kort” värde: − ½ |